为了在磨削加工中避免类似于图6-3中的分岔形式，在砂轮的头架上附加一个非线性的速度反馈控制，用以将亚临界的Hopf分岔转化为超临界的形式。具体来说，选用工件与砂轮相对速度的立方非线性[175]作为负反馈，并通过调节反馈控制的增益来影响颤振的产生形式。与之相应，方程（6-5）中的非线性项f 转变为

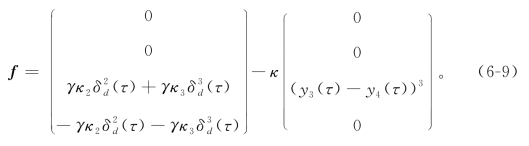
其中κ是无量纲的非线性反馈增益。

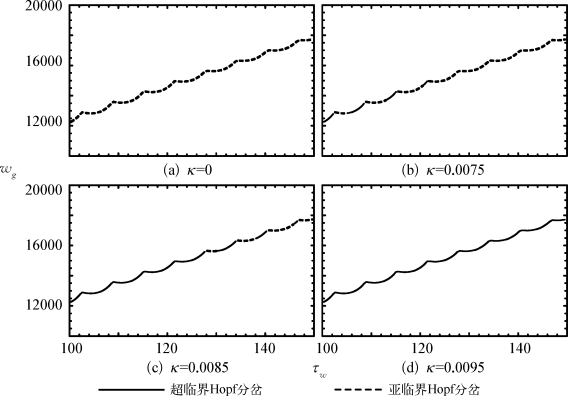
从局部来看，需要将发生在图6-2中的稳定性边界上的亚临界Hopf分岔全部转化为超临界。为此，可以采用多尺度法来计算发生颤振时系统的规范型方程，并观察振幅方程中三次项前面的系数符号，从而判断亚临界的Hopf分岔是否被转化，而这一思想也和第3 章寻找Bautin分岔点的方法一致。相应的计算结果反映在了图6-4中。从图中可以看出，当反馈增益κ为0，即没有施加反馈控制的时候，所关注的稳定性边界曲线上所发生的分岔都是亚临界Hopf分岔。但随着κ的增加，这些局部的分岔行为会被逐渐地转变为超临界的Hopf分岔。从图6-4（d）中看到，当κ增大到0.0095 的时候，所关注的临界边界已全部被转化过来。

从局部来看，增加反馈增益能够帮助我们避开亚临界Hopf分岔。然而，从全局来看，仅仅将亚临界Hopf分岔转化为超临界还不够，我们还需要避免周期解上可能会出现的折分岔，这一点从图6-5中可以看出。图6-5（a）即是图6-3，反映了在不施加控制情况下系统经过亚临界分岔而产生磨削颤振的情况。当增加控制的增益κ，该分岔形式会局部地转化为亚临界，如图6-5（b）。然而，从全局来看，图6-5（b）中的周期解分支上面又继续产生了折分岔，这导致线性稳定的参数区间中依然存在颤振和稳定磨削共存的情况。有所不同的是，这个共存的参数区间有所减小。进一步的增加反馈增益κ直到0.05，周期解上的折分岔逐渐消失，最终形成如图6-5（c）中所示的简单超临界Hopf分岔。因而磨削颤振在工件和砂轮失去接触之前的振幅相对要小得多，且不再存在颤振与稳定磨削共存的情况，从而增加了实际加工中可用的参数区域，也避免颤振总是以大振幅的形式突然出现。

(www.daowen.com)

图6-4　反馈增益对稳定性边界上分岔形式的影响

（a）不施加控制的时候稳定性边界上都是亚临界的Hopf分岔；（b）反馈增益κ为0.007 5，有小部分边界上的分岔形式被转化；（c）反馈增益κ为0.008 5，大部分边界上的分岔形式被转化；（d）反馈增益κ为0.009 5，图中所有边界上的分岔形式都被转化为超临界Hopf分岔。

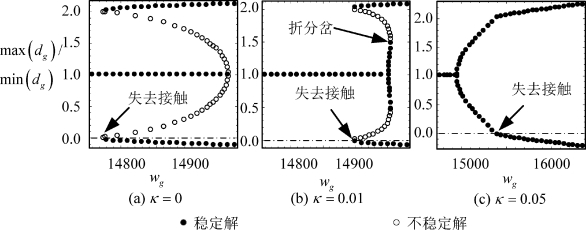
图6-5　反馈增益κ 对全局分岔的影响

（a）κ=0，没有施加控制，颤振以亚临界Hopf分岔的形式产生；（b）κ=0.01，控制增益较小的时候，亚临界的Hopf分岔被局部地转化为超临界分岔，然而周期解分支上的折分岔依然存在；（c）κ=0.05，继续增加反馈增益可以消除掉周期解上的折分岔，从而减小磨削颤振的振幅且避免颤振与稳定磨削共存的情况。

总的来说，不论从控制局部分岔还是控制全局分岔的角度出发，在加工中都应该尽量增大非线性反馈增益，从而减小颤振的振幅且增大可用的参数区域。