接下来求解方程（5-33），从数学上来说，（5-33）是一个Bernoulli方程，因此，我们可以直接得到该方程的解为

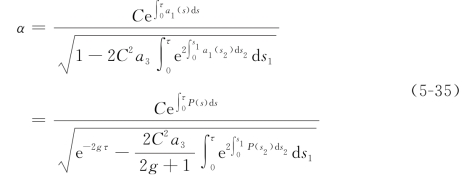
在方程（5-35）中和都是关于时间τ 的周期或者线性函数。因此，由方程（5-35）所决定的颤振振幅α 的长期解由指数函数e-2gτ决定。举例来说，当g＞0，e-2gτ会随着时间τ 而逐渐趋于零，此时α保持为正，颤振依然存在。相反，当g ＜0，e-2gτ会随时间推移而趋于正无穷，相应的颤振振幅α则会趋向于零，这也就意味着原本存在着的颤振被成功抑制下来。

作为一个算例，本书采用该方法去抑制图5-4（a）中所对应的颤振运动。与之相应，此算例中参数a1（τ）的值为

其中，… 代表余下的所有周期函数。

为了知道如何能够将颤振抑制下来，需要先从方程（5-36）中分离出g的值。由于g 代表了a1（τ）中所有的常数项，而方程（5-36）中的5.577 5ε2ΔgΔwcos（φg-φw+εΩgτ-εΩwτ）既可以是周期函数也可以取为常数，这取决于参数Ωg和Ωw的取值：

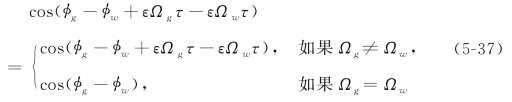
从方程（5-35）中可以知道，最好的抑制颤振的方法是尽量使得g →-∞。再考虑到方程（5-37），最佳的变转速策略则应该为

此时，g 能够取得最小值

(www.daowen.com)

总结起来，最佳的变转速控制策略是让砂轮和工件的转速变化具有相同的频率和半个周期的相位差。在实践中，这一控制策略可以通过用不同的放大器放大同一信号得到。具体来说，在使用正弦控制信号sin（εΩτ）去实时摄动砂轮和工件转速之前，该信号被同时放大εΔg倍和-εΔw倍。再考虑到-Δwsin（εΩτ）=Δwsin（εΩτ+π），我们就得到了两个频率相同而相位相差半个周期的控制信号。

然后基于方程（5-39）来说明变转速颤振抑制的效果。在图5-6中，我们在空间ετwε-εΔg-εΔw中绘制出了g=0的曲面，从而区分开了g ＜0和g ＞0的参数空间。在曲面之下有g ＞0，意味着此参数区域中的颤振没有被抑制下来。而在曲面之上有g ＜0，对应着能够使得颤振运动消失的参数取值。

为了能够进一步说明，我们取了图5-6的一个截面（ετwε=-0.4），并绘制在了图5-7中。该图中的灰色区域代表能够将颤振抑制下来的参数取值，而白色区域代表仍然保持颤振的区域。为了验证这里分析的结果，我们选取了三个参考点，点Ⅰ、Ⅱ和Ⅲ来分析其对应的动力学行为。

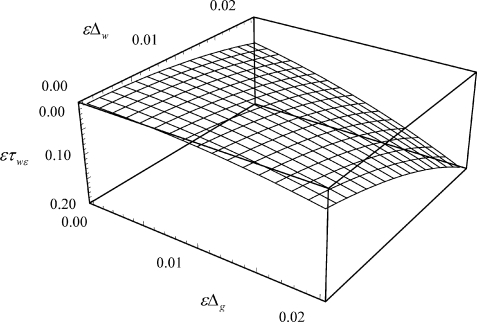
图5-6　临界曲面g=0，该曲面之上有g＜0，其下为g＞0

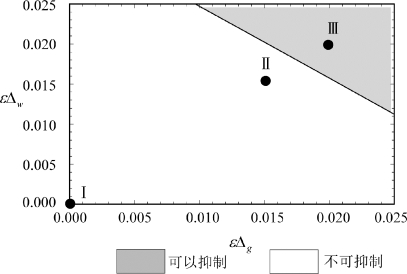
图5-7　ετwε=-0.4时的变转速振幅取值

对图5-7中的点Ⅰ、Ⅱ和Ⅲ，采用数值积分的办法计算了该磨削过程中磨削深度的变化规律。图5-8（a）描绘了没有变转速控制时的颤振运动。在施加了比较弱的变转速控制（εΔw=εΔg=0.015）以后，该颤振运动并没有被抑制下来，而是呈现出图5-8（b）的运动形式。此后继续增大转速变化幅度（εΔw=εΔg=0.02），该颤振最终被成功抑制下来，其时间历程如图5-8（c）所示。

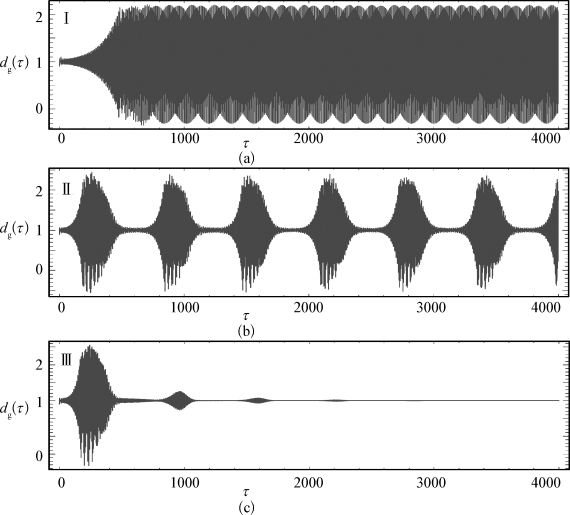
图5-8　对应于图4-7中参数点Ⅰ、Ⅱ和Ⅲ的磨削深度的时间历程图

（a）对应于点Ⅰ（εΔw=εΔg=0），即没有施加变转速控制时的颤振运动，（b）对应于点Ⅱ（εΔw=εΔg=0.015），变转速控制幅度不大时的颤振，（c）对应于点Ⅲ（εΔw=εΔg=0.02），变转速控制幅度增大到能够抑制颤振。