为了研究变转速控制在临界状态附近的效果，引入对稳定性边界上的临界参数值的摄动

式中，κ1c和τwc分别代表参数κ1和τw在临界边界上的取值，无量纲的小量ε意味着对该临界参数的摄动很小。接下来套用多尺度分析方法，将原始时间τ扩展成为不同的时间尺度T0=τ、T1=ετ 和T2=ε2τ。与之相应，常微分算子转变为

与此同时，将方程（5-12）的解y（τ）展开为

对应于新引入的多个时间尺度和被摄动的参数，时滞项可以展开为

其中

y1iτg=y1i(T0-τg,T1,T2),

y2iτw=y2i(T0-τwc,T1,T2),(i=0,1,2)

令，将方程（5-16）、（5-17）、（5-18）和（5-19）代入方程（5-12）并搜集方程中ε1和ε2前面的系数，分别为

和

考虑到方程（5-16），方程（5-20）的解可以写作

其中c.c.代表其前面项的复共轭，iω 对应于稳定边界上临界特征值的虚部，而r=（1，r2，r3，r4）则对应于临界情况时的一个右特征向量。换句话说，它们满足以下方程：

将方程（5-22）代入方程（5-21）后可以得到

其中(www.daowen.com)

且有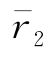代表r2的复共轭。

如前面所说，方程（5-24）有解的充分必要条件是其中的长期项要全部被消除，即其中所有和eiωT0成比例的项都应该被消去。为此，引入一个特解y*1使其满足

根据Fredholm 定理y*1存在的充分必要条件是以下方程满足：

其中l=（1，l2，l3，l4）是对应于临界情况时的一个左特征向量，即它是以下方程的解：

接下来，求解方程（5-26）就可以得到B（T1，T2）所需要满足的微分方程为

在消除了方程（5-24）的长期项以后，可以直接求解方程（5-24）得到

其中

更进一步，继续重复上面的流程。把方程（5-16）、方程（5-17）、方程（5-18）、方程（5-19）、方程（5-22）、方程（5-29）代入方程（5-12）并搜集其中ε3项的系数，然后重复前面的分析流程，即从方程（5-24）到方程（5-28），则可以计算出。之后，通过下面的方程重构振幅函数B 所满足的微分方程

最后，引入极坐标变换

就可以将方程（5-31）的实部和虚部分离为

式中，a1（τ）=g+P（τ）。g 代表a1（τ）中的常数；P（τ）是由变转速控制所引入的时变函数。

显然，方程（5-33）独立，并且其未知数α 代表该颤振过程的振幅，于是可以通过求解该方程去考察磨削的动力学行为：如果α为正则该过程为颤振，而如果α为零则代表没有振动。