第4章指出，工件的第一阶模态最容易被激发出来。此外，Fu[200]的实验还证明，磨削过程中的颤振频谱都主要由工件的低阶模态占据。因此，为了方便起见，下面的分析中仅仅考虑工件最容易被激发出来的模态，即第一阶模态。在考虑边界条件（5-2）的情况下，方程（5-1）中梁的位移可以表示为

考虑方程（5-3）和方程（5-4），将方程（5-5）代入方程（5-1），并采用Galerkin截断，可以得到：

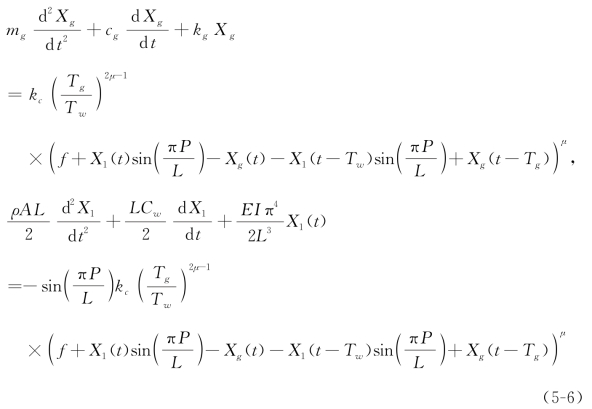
式中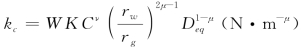，。可以看到，同样是磨削刚度，这里的kc和方程（2-8）中的kc（N·m-1）有所不同，这主要体现实际加工中，磨削力与切削深度的关系是非线性的。此外，方程（5-6）中还出现了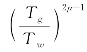，这表明磨削力的大小与砂轮和工件的转速也有关系。

为了后面的分析，进一步简化方程（5-6），将其平衡点移动到坐标原点。为此，引入坐标变换：

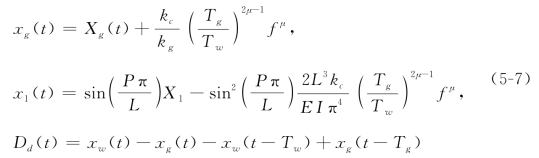(www.daowen.com)

和等效参数

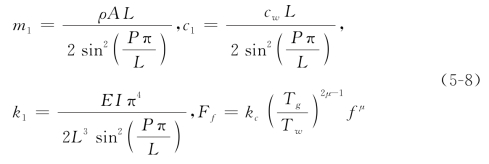
式中，Dd就是切削深度Dg中除去初始进给量以外的动态磨削深度。相应的，就可以将方程（5-6）转变为

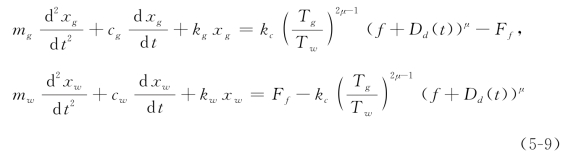
式中，xw（t）为等效的工件位移，（m）；mw为等效的工件质量，（kg）；cw为等效的工件阻尼，（N·s·m-1）；kw为等效的工件刚度，（N·m-1）；Ff（N）为等效的进给力。

可以看到，方程（5-9）是一个等效的数学模型，对应于图5-1中的力学模型。