在往复式磨削加工过程中，砂轮始终沿着工件轴向作往复运动，其位置p也随着时间在0和l之间来回变换。如图4-6所示，砂轮以很慢的速度vg从工件的一段（p=0）移向另一端（p=l）。在到达后折返回来，并以相同的速度回到出发点，而后重复该过程，直到磨削结束。

由于砂轮的移动速度vg非常小，砂轮的位置p 被视为准静态的参数。因此，可以预见该磨削过程中切削深度的时间历程图会一直黏附于前面得到的分岔图。为了证明这一结论，选取了几个比较典型的情况以方便进一步的数值分析。这些情况为

图4-6　砂轮的位置p 在往复式磨削过程中不断改变

情况Ⅰ：τw=84，情况Ⅱ：τw=80，情况Ⅲ：τw=80.8，

情况Ⅳ：τw=82.6，情况Ⅴ：τw=68，情况Ⅵ：τw=68.34。

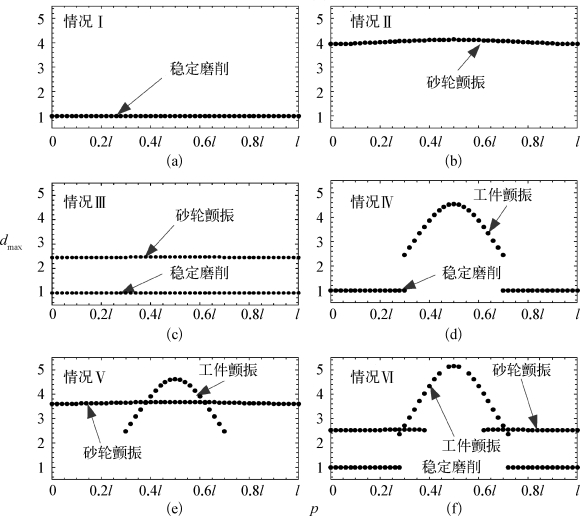
对应不同的情况，将其分岔图绘制在了图4-7中。图4-7（a）反映了该磨削过程始终保持稳定，不论砂轮移动到何处。与之相反，图4-7（b）中的磨削过程始终保持工件颤振。在图4-7（c）中，前面所提到的两种情况同时出现，因此，决定该磨削过程中的动力学行为的因素变成了该磨削过程的初始状态。与砂轮颤振相比，工件颤振的分布情况要特别得多。图4-7（d）、（e）和（f）反映了工件颤振的情况仅存在于砂轮在工件中点附近移动的时候。而具体说来，图4-7（d）体现了工件颤振和稳定磨削状态之间的来回切换，而4.7（e）则反映了工件颤振与砂轮颤振的共存。最后，图4-7（f）中同时出现了三种可能的磨削动力学行为。

(www.daowen.com)

图4-7　最大磨削深度dmax关于砂轮位置p 的变化规律

（a）情况Ⅰ（τw=84），稳定磨削过程；（b）情况Ⅱ（τw=80），砂轮颤振；（c）情况Ⅲ（τw=80.8），稳定磨削与砂轮颤振共存；（d）情况Ⅳ（τw=82.6），稳定磨削与工件颤振共存；（e）情况Ⅴ（τw=68），砂轮颤振与工件颤振共存；（f）情况Ⅵ（τw=68.34），稳定磨削，砂轮颤振和工件颤振同时存在。

得到了分岔图4-7后，就可以利用该图去追踪砂轮移动对磨削动力学行为带来的影响。具体来说，基于图4-6寻找砂轮位置关于时间的变化规律，然后通过图4-7建立颤振振幅随时间的变化规律，从而得到磨削颤振的动力学行为。最后，为了验证该结果，对原方程直接进行数值积分，并将分岔图嵌入直接数值积分得到的时间序列中，见图4-8中。

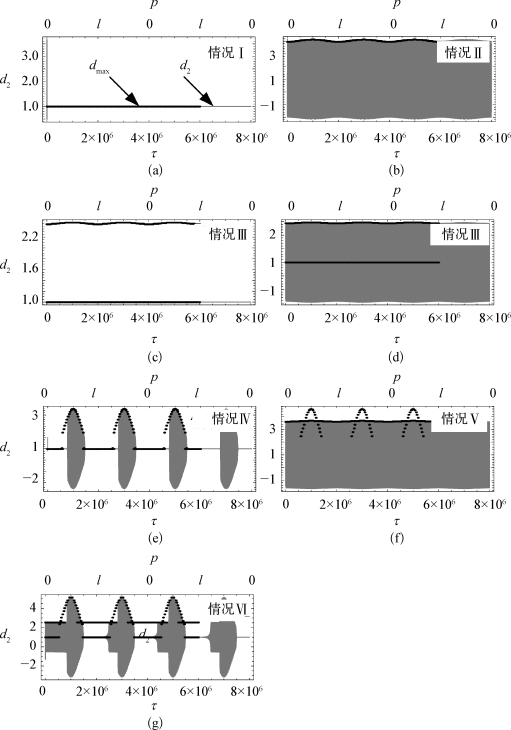
图4-8　切削深度d2的时间历程图，图中还嵌入了颤振振幅dmax关于砂轮位置的分岔图p

（a）情况Ⅰ（τw=84），磨削过程始终稳定；（b）情况Ⅱ（τw=80），砂轮颤振；（c）情况Ⅲ（τw=80.8），稳定磨削过程；（d）情况Ⅲ（τw=80.8），砂轮颤振；（e）情况Ⅰ（τw=82.6），工件颤振和稳定磨削过程之间不断切换；（f）情况Ⅴ（τw=68），虽然工件颤振的分岔图存在，但仅有砂轮颤振出现；（g）情况Ⅵ（τw=68.34），稳定磨削、砂轮颤振和工件颤振之间不断切换。

图4-8中，可以清楚地看到，磨削深度d2的时间历程图被静态分析得到的颤振振幅dmax的分岔图所包络。图4-8（a）显示了稳定的往复式磨削过程，而图4-8（b）中则全程都是砂轮颤振。在图4-8（c）和（d）中，我们看到相同的参数取值情况下可能出现截然不同的磨削动力学行为，分别是稳定磨削和砂轮颤振。图4-8（e）反映了工件颤振的情况，可以看出这种形式的颤振运动是间歇性的，颤振出现在砂轮靠近工件中心时，消失于砂轮向工件两端移动的时候。在图4-8（f）中，再次观察到了类似于图4-8（b）和（d）中的砂轮颤振运动，尽管它们所对应的分岔图是截然不同的。最后，图4-8（g）描述了最为复杂的一种情况，即磨削过程的动力学行为会在稳定磨削、砂轮颤振和工件颤振之间来回切换。但仍然可以看到，颤振依旧产生于砂轮移动到工件中点附近的时候。

总而言之，利用准静态分岔分析得到的结果能够很方便地构造出整个往复式磨削过程中系统可能产生的各种不同的颤振行为。结果表明，往复式磨削中的砂轮颤振是连续的而工件颤振则是间歇性的。