如前面所分析的，仅有工件的低阶模态的振动会被磨削力激发，因此，本书接下来的内容会侧重研究这之中最为危险的一项，即工件的第一阶模态。根据方程（4-32），我们事先假设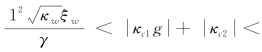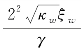。与之相应，方程（4-17）和方程（4-18）中仅考虑n=1的情况。

作为一个算例，如下选取原方程中的物理参数：

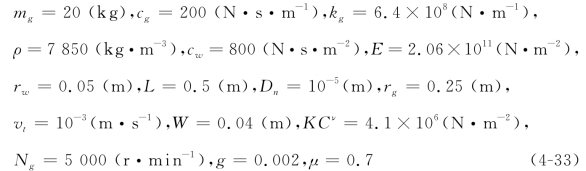
与之相应，可以得到

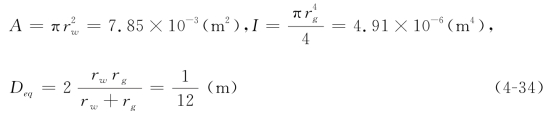
接下来通过方程（4-14）计算系统的无量纲参数可以得到

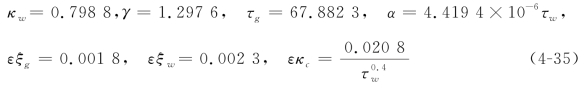(www.daowen.com)

在有了具体的参数值以后，可利用方程（4-31）在图4-3中绘制出了系统的稳定性边界（实线）。此外，为了验证该结果的正确性，同时采用第2章中的延拓算法得到了数值的结果，并将其一同绘制在了图4-3中（点）。可以看到，理论分析与数值计算的结果拟合得非常好，这也就证实了本书的理论分析的正确性。

图4-3反映了砂轮的位置p 和时滞τw对磨削稳定性的影响。当参数落在稳定区域中（灰色）时，该磨削过程平稳，而当参数落在颤振区域（白色）中时，磨削过程失稳且产生磨削颤振。此外，图4-3中还标出两种不同的颤振区域，分别是砂轮颤振和工件颤振区域。在砂轮颤振区域中，方程（4-31）的第一个稳定性条件被破坏，对应于砂轮失稳且开始振动。而在工件颤振区域中，方程（4-31）的第二个稳定性条件被破坏，意味着工件第一阶模态的振动被激发。

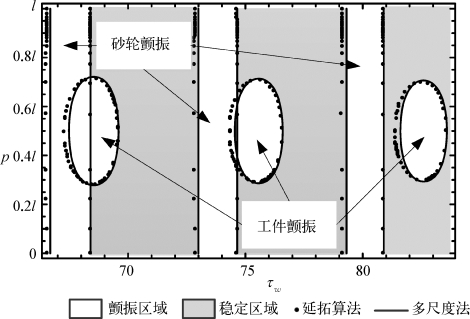
图4-3　参数平面上分离颤振区域和稳定区域的稳定性边界。该磨削过程在稳定区域中（灰色）是稳定磨削过程，而在颤振区域中（白色）不稳定且会产生颤振。图中的实线由多尺度算法得到，而点则由延拓算法得出

更进一步的，从图4-3中还可以看出，砂轮的稳定性与工件的位置p 几乎没有任何关系，但工件的稳定性却与p 的取值密不可分。当砂轮靠近工件中心时，图4-3中的稳定性区域最小，也就对应了该磨削过程的稳定性最差。

针对以上结果，必须要指出的是图4-3和图2-5中的时滞τw的取值范围有很大的不同。图2-5中的τw取值仅限于101量级，而图4-3中的τw则取到了102量级。实际上这样的区别在实际加工过程中也是完全有可能会遇到的，由于τw体现的是工件的主轴转速，根据加工对象和目标精度的不同，其取值会有较大范围的改变，例如型号为M1332B 的外圆磨床的工件主轴转速可以在27 r/min到313 r/min的范围内进行调节。此外，考虑到第4章中砂轮刚度kg的取值和第2、3章中有很大的差距，由此无量纲的时滞τw也会相差较多。由此二者可知，图4-3和图2-5中的时滞τw的取值均在合理的范围以内。