多尺度方法分析磨削稳定性中的摄动效应

时间：2023-07-02 理论教育 版权反馈

【摘要】：为了理论地分析磨削稳定性，这里采用多尺度方法。与前一章一样，该方法引入多重时间尺度T0=τ 和T1=ετ，并且将方程的解展开为其中i代表g，1，2，…在方程中，αg代表砂轮的振幅而αi（i=1，2，…同样，工件的第i阶模态稳定的条件是方程中对应的αi前面的系数分别为负。显然，由于，方程的左端应满足从方程可以看出，工件高阶模态的稳定性条件不会被破坏，即再生力仅会诱发工件低阶模态的颤振。

多尺度方法分析磨削稳定性中的摄动效应

为了理论地分析磨削稳定性，这里采用多尺度方法。与前一章一样，该方法引入多重时间尺度T0=τ 和T1=ετ，并且将方程（4-18）的解展开为

其中i代表g，1，2，…，n。相对应的，关于时间的导数和时滞项展开为

pagenumber_ebook=86,pagenumber_book=68

其中i代表g，1，2，…，n，而j代表g，w。接下来，将方程（4-21）代入方程（4-18）并分别收集其中ε0和ε1前面的系数，得到

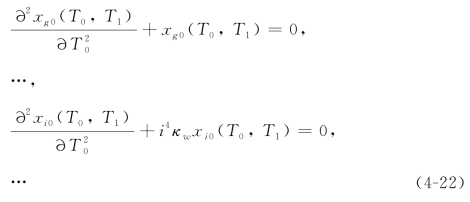
pagenumber_ebook=87,pagenumber_book=69

和

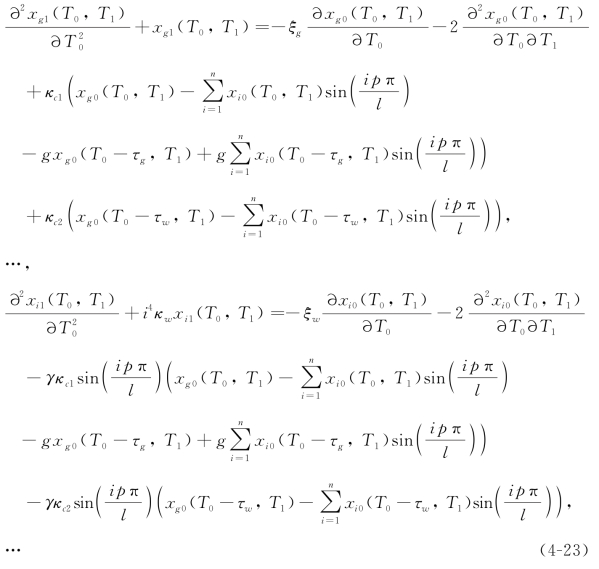
pagenumber_ebook=87,pagenumber_book=69

其中i代表g，1，2，…，n。

显然，方程（4-22）的解可以写成如下形式

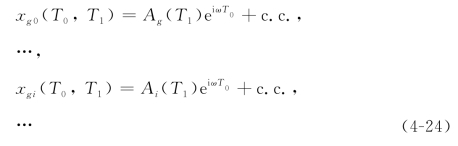
pagenumber_ebook=88,pagenumber_book=70

其中代表其前面所有项的复共轭。将方程（4-24）代入方程（4-23）得到

pagenumber_ebook=88,pagenumber_book=70

其中i代表g，1，2，…，n。

根据Nayfeh[130，206]的方法，方程（4-25）的解存在的充分必要条件是其右端的所有共振项全部被消除，而这里所谓的共振项即是所有与eiωiT0（i代表g，1，2，…，n）成正比的项。因此，为了消除所有的共振项，Ai（T1）（i代表g，1，2，…，n）应该满足

pagenumber_ebook=89,pagenumber_book=71

其中i代表1，2，…，n。将方程（4-26）重新排列可以写作(www.daowen.com)

pagenumber_ebook=89,pagenumber_book=71

其中i代表1，2，…，n。

接下来，为了将复振幅Ai（T1）（i代表g，1，2，…，n）展开，引入如下极坐标变换：

其中i代表1，2，…，n。将方程（4-28）代入方程（4-27）并分离其实部和虚部，分别得到

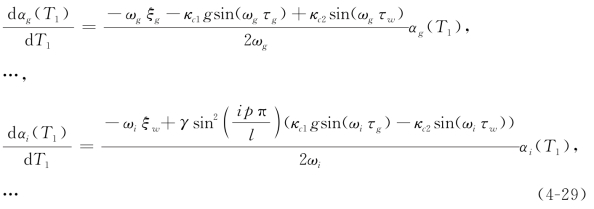
pagenumber_ebook=90,pagenumber_book=72

和

pagenumber_ebook=90,pagenumber_book=72

其中i代表1，2，…，n。在方程（4-29）中，αg（T1）代表砂轮的振幅而αi（T1）（i=1，2，…，n）代表工件的各阶模态的振幅。

从方程（4-29）中，很容易找出该磨削过程的稳定性条件。例如，砂轮稳定的条件是方程（4-29）的第一个方程中αg（T1）前面的系数为负。同样，工件的第i阶模态稳定的条件是方程（4-29）中对应的αi（T1）前面的系数分别为负。简单来说，整个磨削过程保持稳定的条件为

pagenumber_ebook=90,pagenumber_book=72

其中i=1，2，…，n。

显然，由于，方程（4-31）的左端应满足

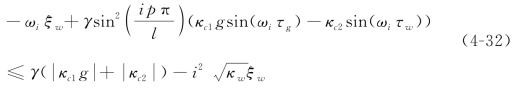
pagenumber_ebook=91,pagenumber_book=73

从方程（4-32）可以看出，工件高阶模态 pagenumber_ebook=91,pagenumber_book=73 的稳定性条件不会被破坏，即再生力仅会诱发工件低阶模态的颤振。此外，随着磨削刚度的增大，更多工件模态的振动会被激发。例如，当，工件的振动不会被激发，而当时，工件前n阶模态的振动都有可能被激发。与这个结论相关的实验结果在Fu[200]的论文中有所体现。在他的研究中，磨削颤振仅仅包含了工件的最低三阶模态的振动。