在说明了系统的控制方程以后，接下来开始分析该磨削过程的动力学特性。首先分析最为简单的情况，即稳定磨削过程。考虑到边界条件，即方程（4-2），方程（4-1）的解可以展开为

当颤振没有发生时，由方程（4-8）所表示的解与时间t无关，此时可将静态的砂轮和工件位移记为Xg（t）=和Xw（t，S）=（S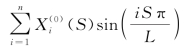）=。相对应的，方程（4-1）被简化为

其中是砂轮和工件之间的静态相对位移。

接下来，将方程（4-9）两端乘以并将其从0积分到L，得到

其中i=1，2，…，n。很容易从方程（4-10）得到(www.daowen.com)

显然，方程（4-11）是静态相对位移Δ（0）（P）的隐函数，可以用数值的办法求解。在利用方程（4-11）求得Δ（0）（P）以后，可以再利用方程（4-10）分别解出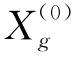和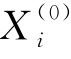（i=1，2，…，n）。

从物理上来说，这里得到的静态位移反映了稳态磨削过程中砂轮和工件各自的平衡位置，而从数学上来说，静态位移对应了方程（4-1）的平衡点。相对应的，如果平衡点稳定则该稳态磨削过程稳定，而平衡点失稳则意味着磨削过程失稳并诱发颤振。为了进一步分析系统的稳定性和颤振运动，需要将方程（4-1）的平衡点移动到坐标原点，为此引入如下的变量

其中i=1，2，…，n。相对应的，方程（4-1）变为