在磨削加工开始之前，砂轮向工件方向进给直到达到名义磨削深度Dn（m）。然而，真实的磨削深度Dg除了包含Dn，还需要考虑由砂轮和工件之间的磨削力Fg所引起的让刀现象。因此，该磨削过程中的实时磨削深度和砂轮与工件的径向相对位置Δ（t，P）=Xw（t，P）-Xg（t）（m）密切相关。

如图4-2中所示，往复式磨削过程中砂轮和工件的接触区域被划分为区域Ⅰ和Ⅱ。在区域Ⅰ中，已经被磨损的砂轮在磨削还没有被磨削过的工件表面，因此，区域Ⅰ中的磨削深度Dg与砂轮的磨损和砂轮工件的当前相对位置有关Δ（t，P）。而在区域Ⅱ中，正在被磨削的工件表面是由上一轮磨削再生的表面，因此区域Ⅱ中的磨削深度还与工件旋转一个周期之前砂轮与工件的相对位置Δ（t-Tw，P）有关。总结起来，动态磨削深度由下面方程给出：

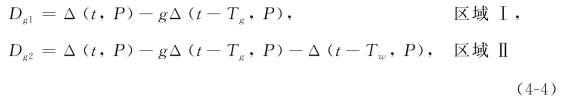
式中，Tg（s）和Tw（s）分别是砂轮和工件的旋转周期。

图4-2　砂轮与工件的相互作用。磨削力同时产生于它们的接触区域Ⅰ和区域Ⅱ之中，区域Ⅰ中的再生效应仅存在于砂轮表面，而区域Ⅱ中的再生效应同时存在于砂轮和工件表面

在方程（4-4）中，Δ（t-Tw，P）代表区域Ⅱ中工件表面的再生效应。具体来说，此时被砂轮所切下来的切屑的上表面是工件旋转一个周期之前的切屑下表面。因此，在即时切削深度表达式中必须考虑工件表面再生的影响。相似的，gΔ（t-Tg，P）代表了砂轮表面的磨损（即砂轮的表面再生效应），其中g 是一个无量纲的系数，反映了磨削过程中砂轮的损耗速度远远低于工件的磨损速度。一般情况下，g 的取值范围为，说明砂轮的硬度很高，不易损耗，而1则代表砂轮很软，其损耗速度和工件一样[233]。

除了磨削深度Dg，在计算磨削力前还需要确定磨削宽度W。观察图4-2，考虑砂轮的转速和轴向移动速度，则区域Ⅰ和Ⅱ中的磨削宽度分别为(www.daowen.com)

式中，vg为砂轮的轴向移动速度，（m·s-1）；α为一个无量纲的比例系数，。

同时考虑方程（4-3）、方程（4-4）和方程（4-5），可以得到区域Ⅰ和Ⅱ中的磨削力表达式分别为

和

式中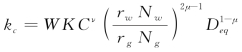，。总的来说，砂轮和工件直接的磨削力为Fg=Fg1+Fg2。