前面通过理论和数值的办法，详细讨论了由超临界Hopf分岔所诱发的周期性颤振运动。然而，进一步的研究表明，在参数区域中，还同时存在着亚临界的Hopf分岔。为了说明这一情况，将图2-7（b）重新绘制在图3-3中，并标记了箭头D 和E来帮助后面的分析。

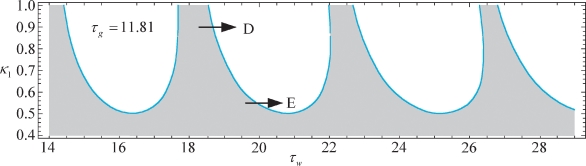
图3-3　稳定性边界

沿着箭头D 和E，利用DDEBIFTOOL[204]对系统的动力学行为作了分岔分析，相应的结果在图3-4中。图3-4（a）显示了与前一节中相同的超临界Hopf分岔的情况，可以看到，该磨削过程的稳定区域和颤振区域被线性分析得到的稳定性边界清晰地分开。因此，对应于超临界Hopf分岔的情况，只需要对系统进行第2章中的线性分析就足以了解磨削过程的稳定性和颤振运动。然而图3-4（b）又表明该过程中还同时出现了亚临界Hopf分岔的情况，此时，在磨削稳定区域和颤振区域之间又出现了一个所谓的条件稳定区域，即该参数区域中的磨削动力学行为还取决于系统的初始状态。在相同的参数情况下，系统可以是稳定也可以是颤振，如图3-4（d）和（e）所示。

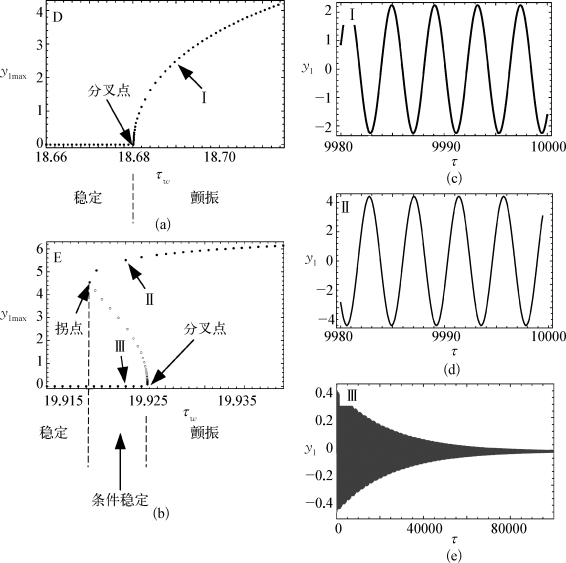
图3-4　分岔图和时间历程图

（a）参数沿箭头D变化时颤振振幅y1max的变化规律，（b）参数沿箭头E变化时颤振振幅y1max的变化规律，（c）对应于参数点Ⅰ时y1的时程图，（d）对应于参数点Ⅱ时y1的时程图，（e）对应于参数点Ⅲ时y1的时程图。

可以看出，图3-4（b）中重要的不仅仅是由线性分析得到的临界参数，还必须考虑在分岔出来的周期运动分支上的拐点，而这两个点之间所夹的区域就是条件稳定区域。此外，在这两个点重合的时候，也就是超临界Hopf分岔和亚临界Hopf分岔转变的时候，这个点被称作Bautin分岔。因此，为了准确地找出条件稳定区域，这里需要进行Bautin分岔的分析。

Bautin分岔点位于Hopf分岔曲线上，因此有εκ1ε=0和ετwε=0，相应地可以得到

此时，方程（3-37）变为(www.daowen.com)

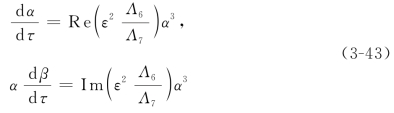
此外，为了满足Bautin分岔的条件，方程（3-43）的第一条方程中α3的系数也必须为零，即

为了找到该Bautin分岔点，需要同时求解方程（3-3）、方程（3-4）和方程（3-44），得到的结果记录在表3-1中。

表3-1　Bautin分岔点

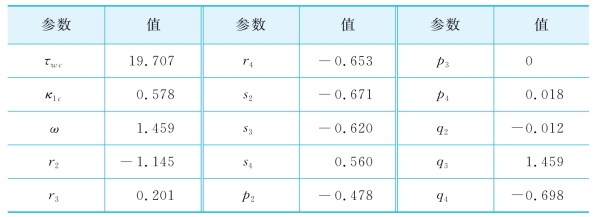
Bautin分岔点仅仅是条件稳定区域的起点，为了更准确地划分出该区域，继续使用DDEBIFTOOL，从Bautin点出发沿着图3-3中的临界曲线去连续地寻找各个周期解分支上的拐点。最后将这些拐点记录下来并连接成曲线，得到了图3-5中的分岔图。

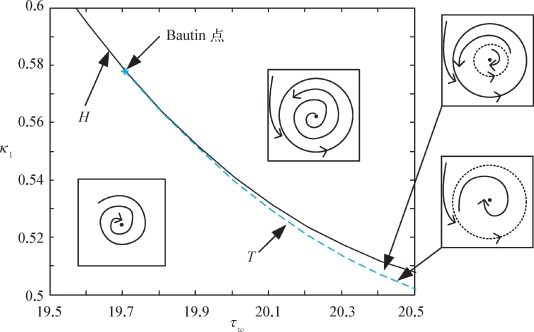
图3-5　Bautin分岔图

图3-5中的参数区域被两条曲线分割，分别是实线H 和虚线T，其中实线H 是在线性分析中就得到的稳定性边界曲线，而虚线T 则是由周期解上的拐点构成。如图中所示，曲线H 和T 下方的区域属于稳定区域，H上方的区域是颤振区域，而夹在H 和T 之间的区间则是条件稳定区域。如前面所述，条件稳定区域中的动力学行为取决于磨削过程的初始条件，它最终可能是稳定的磨削，亦可能产生再生颤振。

对于实际的加工过程，人们总希望磨削过程能够保持稳定，而不希望颤振产生。所以，由Bautin分岔产生的条件稳定区域在实际中是不可用的参数区域，即便是这些区域在之前的线性分析中是稳定的。因此，相比于超临界Hopf分岔的情况，条件稳定区域的存在使得在分析磨削动力学的研究中很有必要考虑非线性的因素。