在得到了规范型方程（3-35）以后，接下来就可以通过讨论振幅B（T1，T2）来研究磨削颤振的产生过程。引入极坐标变换：

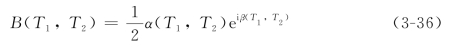
将方程（3-36）代入方程（3-35）并分离其实部与虚部，可以得到

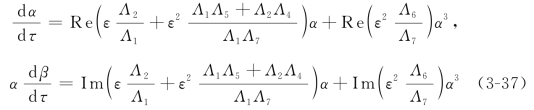
其中，α=α（T1，T2），β=β（T1，T2），而Re（·）和Im（·）则分别代表·的实部和虚部。

由方程（3-24）可知，方程（3-37）中的α和β分别代表了颤振运动近似解的振幅以及频率修正项。显然，方程（3-37）中的α 存在两个不同的稳态解使得，它们是分别代表磨削稳定和磨削颤振的

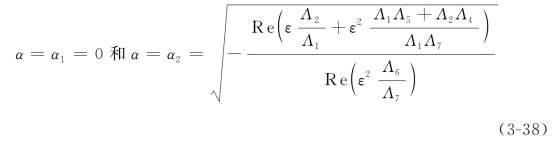
接下来通过讨论α的解的稳定性，我们就可以得到颤振运动的稳定性。

简单来说，当时，解α1稳定，这对应于前一章讨论的稳定磨削过程，此时没有颤振运动产生。而当时，该磨削过程开始失稳，颤振产生，此时振幅α将会逐渐增大。如果再有，则α将会稳定于α2，这就是周期性的颤振的振幅，称这里发生了超临界Hopf分岔。

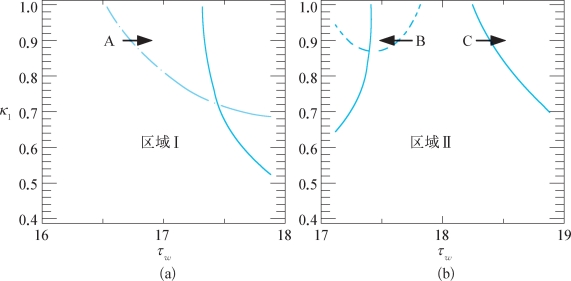
下面就用几个例子来说明这种形式的颤振运动，例如将图2-7中的区域Ⅰ和Ⅱ放大并绘制在图3-1中。此外，图3-1中还标记了箭头A、B 和C以方便后面的分析。

(www.daowen.com)

图3-1　放大的稳定性边界及箭头标记

箭头A：κ1=0.9、τg=14、τwc=16.732、ω=1.678，
箭头B：κ1=0.9、τg=11.6、τwc=17.638、ω=1.048 5，
箭头C：κ1=0.9、τg=11.6、τwc=18.391、ω=1.531。

顺着图3-1中的各个箭头，对应于方程（3-9）中有εκ1ε=0，系统的参数由稳定区域滑向不稳定区域，而磨削过程也相应地由稳定磨削转变为颤振运动。对应于箭头A、B和C，我们利用方程（3-37）得到的稳定的颤振运动的解分别为

和

由于箭头A、B和C 对应于穿过不同的稳定性边界的情况，于是它们触发了不同的颤振模态。再由方程（3-39）、方程（3-40）和方程（3-41）可知，这些不同颤振模态的频率和振幅也大不相同。例如箭头A 所对应的颤振振幅约为箭头B所对应的颤振振幅的十倍。再有一个比较有意思的结果是，方程（3-39）、方程（3-40）和方程（3-41）中的越大振幅颤振对应了越高的振动频率。由于在物理上高的振幅和频率都对应了高的能量，可以知道这些不同的周期性颤振所具有的振动能量也相差很多，因此，磨削加工过程中的参数选择对于降低颤振运动的强度也至关重要。

为了验证前面得到的理论结果，用XPPAUT[230]对原方程做了数值积分，并比较了数值和理论的结果，这些结果都被绘制在了图3-2中。其中，图3-2（a）、（b）和（c）对应于箭头A、B和C的分岔图，反映了颤振振幅y1max和参数τw之间的关系。图3-2（d）、（e）和（f）是系统中可能产生的颤振时间序列，对应于分岔图中三个不同的点，而图3-2（g）、（h）和（i）则是与时间序列相对应的相图。从该图中可以看出，理论分析的结果和数值积分的结果吻合得非常好。此外，从相图3-2（g）、（h）和（i）还可以看出，在颤振发生的时候砂轮和工件的位移呈现相对运动的趋势，这类似于一种反同步的运动。这一点意味着颤振过程中砂轮和工件的相对位置y1-y2变化会比较大，从而磨削深度和切削力的变化幅值也会相对较大。

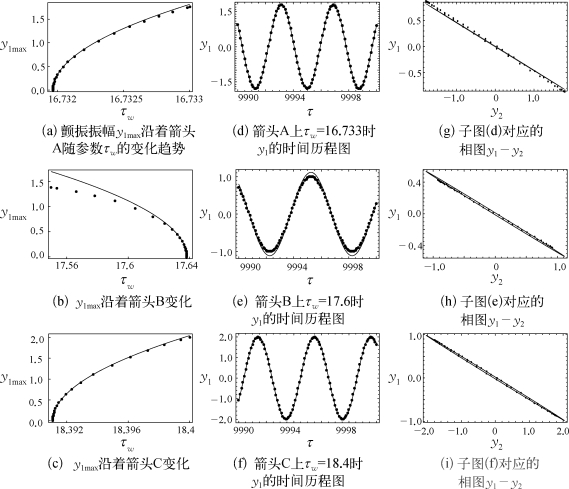
图3-2　分岔图（左列）、时间历程图（中列）和相图（右列），其中实线代表由方程（3-39）、方程（3-40）和方程（3-41）所表示的理论结果，而点则代表数值积分的结果