下面采用多尺度方法对颤振运动进行摄动分析。首先，对应于方程（2-13）中的特征矩阵M，将其改写为

其中，MR和MI都是由实数元素构成的矩阵，分别代表特征矩阵的实部和虚部。此外，对应于每一个特征值λ，都有相应的左、右特征向量：

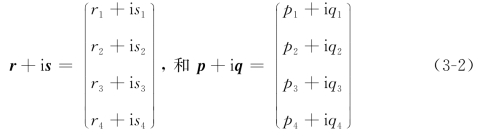
它们满足

和

一般来说，满足方程（3-3）和方程（3-4）的左右特征向量有无穷多种选择。因此，为了使分析过程唯一，需要对左、右特征进行某种归一化，在这里选择r1=1、s1=0、p1=1和q1=0。如此一来，所选用的特征向量就有了唯一性。

在系统参数处于稳定性边界上的时候，有λ=±iω，此时，系统的动力学行为可以用摄动法进行预测。首先，需要引入不同的时间尺度T0=τ、T1=ετ和T2=ε2τ，其中，ε是一个远小于1的无量纲参数，用来在摄动分析中帮助匹配不同的量级。与之相应，状态变量y（τ）对于时间τ的导数则变为

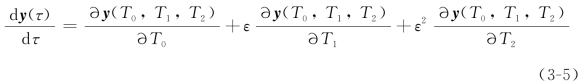
其中

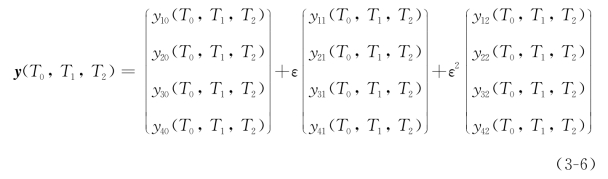
而时滞项yg（τ-τg）和yw（τ-τw）则变为

和

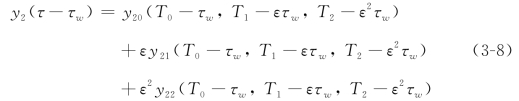
为了保证摄动分析是在临界参数附近进行，需要对所关心的参数在其临界值附近进行摄动。对应于图2-7中的各条临界曲线，分别如下摄动参数κ1和τw：

其中，κ1c和τwc分别代表系统处于临界状态时参数κ1和τw的临界值，而εκ1ε和ετwε则代表对这两个参数在其临界值附近对它们进行了小范围的摄动。接下来，将方程（3-7）和方程（3-8）进行Taylor展开并保留其ε低阶项，得到

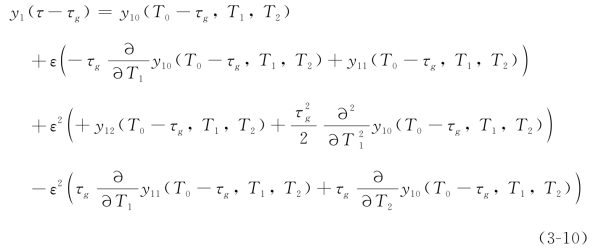
和

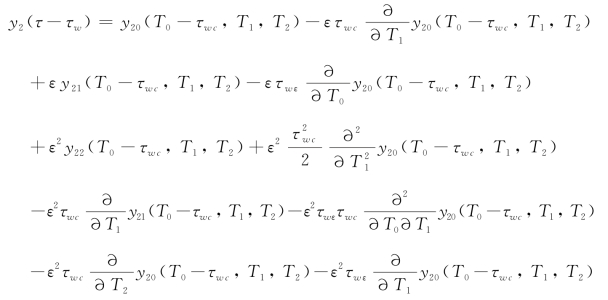
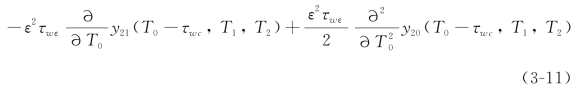
下面将方程（3-5）、方程（3-6）、方程（3-9）、方程（3-10）和方程（3-11）全部代入切入式外圆磨削的控制方程（2-11），然后按照ε的量级分别提取ε0、ε1和ε2的系数项，可以得到下面的一系列方程组。ε0的系数为

和

ε1的系数为

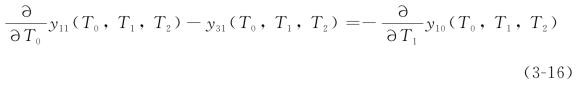
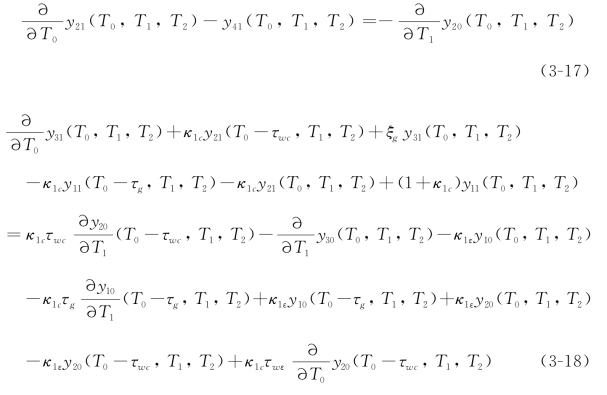
和

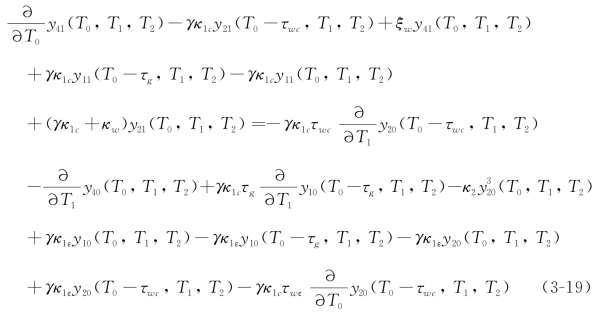
以及ε2的系数

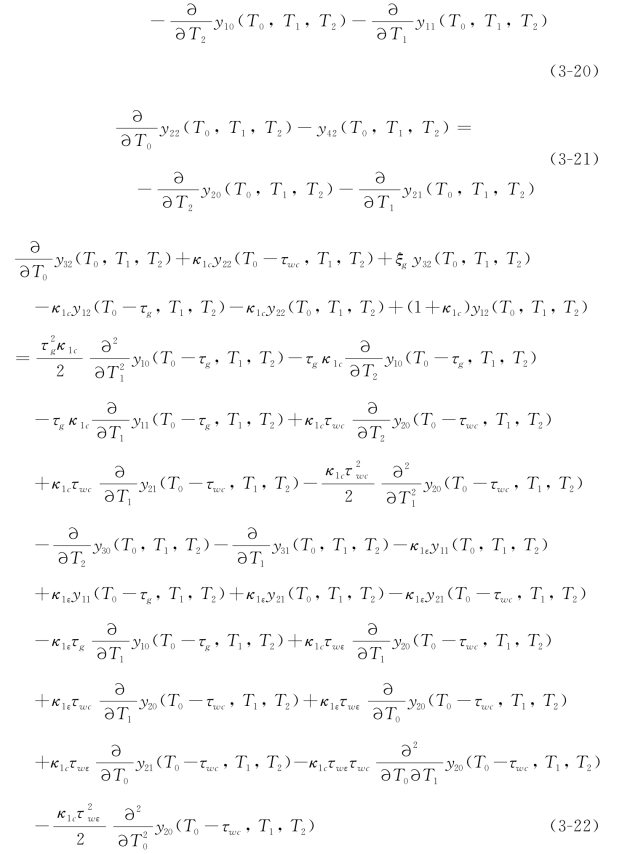
和

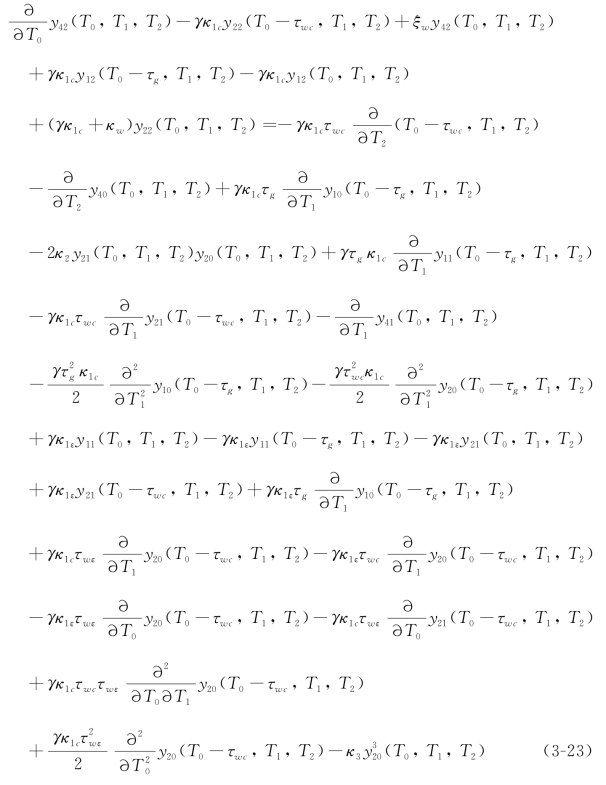
由于这里讨论的是临界曲线附近的情况，再结合方程（3-4），可以知道方程组（3-12）、方程组（3-13）、方程组（3-14）和方程组（3-15）的解具有以下形式：

其中，c.c.代表它前面所有项的复共轭，而ω 对应于临界特征值λ=iω 的虚部，也对应于颤振发生时其线性部分的频率。

将方程（3-24）代入方程组（3-16）、方程组（3-17）、方程组（3-18）和方程组（3-19），得到

(www.daowen.com)

其中，ST1被称为共振项，即是与e-iωT0成正比的所有项，在这里，它由下面方程给出：

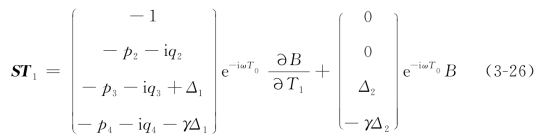
式中

Δ1=-κ1cτge-iωτg+(p2+i q2)τwcκ1ce-iωτwc,

Δ2=(e-iωτg-1)κ1ε+(p2+i q2)(κ1ε+(iωκ1cτwε-κ1ε)e-iωτwc)

B 代表B（T0，T1），而NST1则代表所有剩下的非共振项。

根据Nayfeh提出的多尺度方法[206]，为确保方程（3-25）的解中不存在长期项，其中的ST1必须被消除。为此，给方程（3-25）引入一个特解：

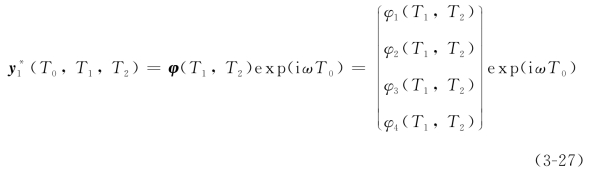
并且让它满足

根据Fredholm 定理，y*1（T0，T1，T2）存在的充要条件（即可解性条件）是

采用以上方法，共振项ST1全部被消除，我们直接求解方程（3-25），得到

其中，代表B（T1，T2）的复共轭且

Δ3=κ2(p2+i q2)2(4ω2-1-κ1c-2iωξg+κ1ce-i2ωτg)(-2iγκ1cξgωe-2iωτwc

+4γκgω2e-2iωτwc-γκ1ce-2iωτwc+2iγκ1cξgω-4γκ1cω2+γκ1c

-2iκ1cξwωe-2iωτg+2iκwξgω+2iκ1cξwω+4κ1cω2e-2iωτg-κ1cκwe-2iωτg

-4κ1cω2-4κwω2+κ1cκw+κw-8iξgω3-8iξwω3-4ξgξwω2

+2iξwω+16ω4-4ω2)-1

仿照前面的分析过程，将方程（3-24）和方程（3-30）代入方程组（3-16）、方程组（3-17）、方程组（3-18）和方程组（3-19）后可以得到

其中，共振项是

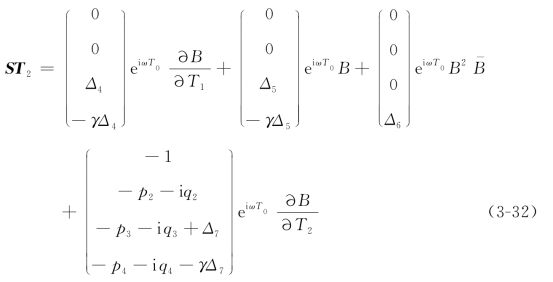
式中

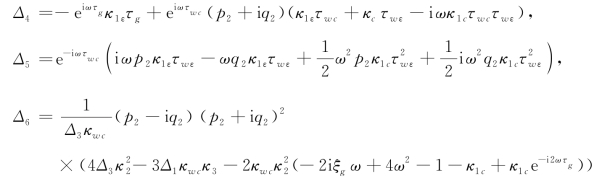
然后我们用同样的方法去消除共振项ST2，得到的可解性条件为

接下来从两个可解性条件，即方程（3-29）和方程（3-33）中可以求解出

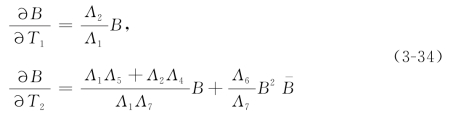
其中

Λ1=1+(r2+i s2)(p2+i q2)+(r3+i s3)(p3+i q3-Δ1)

+(r4+i s4)(p4+i q4+γΔ1)

Λ2=(r3+i s3)Δ2-γ(r4+i s4)Δ2

Λ4=(r3+i s3)Δ4-γ(r4+i s4)Δ4

Λ5=(r3+i s3)Δ5-γ(r4+i s4)Δ5

Λ6=(r4+i s4)Δ6

Λ7=1+(r2+i s2)(p2+i q2)+(r3+i s3)(p3+i q3-Δ7)

+(r4+i s4)(p4+i q4+γΔ7)

最后，由方程（3-34）可以重构出B 所满足的方程为

在数学上，方程（3-35）被称作规范型[231]，可以帮助分析系统中可能出现的动力学行为。在接下来的分析中，将基于规范型方程（3-35），继续讨论切入式磨削加工过程中不同的颤振运动。