在利用上面的延拓算法探讨磨削稳定性之前，需要确定系统的参数值，而在这里被选用的物理参数如表2-1所列。

表2-1　固定的物理参数值

表2-1中的参数均可以还原为实际的工况，相应的无量纲参数可以用方程（2-10）计算得到，如表2-2所列。

此外，在图2-3所示的延拓算法中，还需要先确定非固定参数κ1-τg-τw的取值范围，相应的取值都记录在表2-3中。

表2-2　固定参数对应的无量纲量

表2-3　磨削力参数取值范围

根据图2-3，在确定了固定的参数值以及变化参数的取值范围以后，还需要有方程的两个解作为延拓的起点。为此，可以引入一个新的函数来辅助寻找延拓的起始点。通过引入函数

可以消除方程（2-16）和方程（2-17）中的τw。根据三角恒等式sin2（ωτw）+cos2（ωτw）=1 可以知道，若方程（2-16）和方程（2-17）的解存在，则方程F（ω）=0有解，否则其解不存在，同时系统的临界特征值也就不存在。于是，将另外两个参数κ1和τg固定下来以后，绘出F（ω）与ω 的关系，可以得到图2-4。从图2-4中可以找到方程F（ω）=0的解，从而估计出满足方程（2-16）和方程（2-17）的ω 的取值范围。这之后，将ω 的值代入方程（2-16）和方程（2-17），则可以求出参数τw的值。这些结果将被用作后续延拓算法的起始点。例如图2-4（a）中，当κ1=1而τg=11.3的时候，可以找到ω 的一个解为1.099，再将其代入方程（2-16）或方程（2-17）中，我们得到所求的τw可以取值为16.304。更多的相应结果列在了表2-4中。

表2-4　延拓起始点(www.daowen.com)

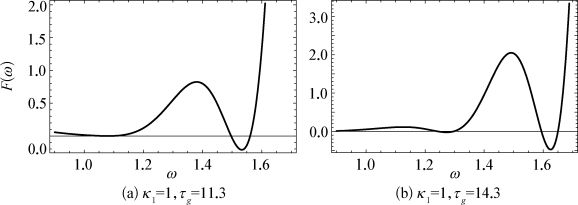
图2-4　F（ω）

以表2-4中的结果作为起点，采用图2-3中所描述的延拓算法，可以在参数空间中依次找出分割磨削稳定和不稳定区域的临界曲面，相应的结果绘制在了图2-5中。可以看出，图2-5中的各个曲面代表了临界特征值λ=±iω 存在的参数区域。其中，不同的曲面分别由不同的起点延拓而出，不仅如此，颜色相同的曲面还代表了这些临界曲面上的特征值ω 的取值是一致的。为了能够进一步地看清参数空间中的磨削稳定和不稳定区域，下面用一系列的截面来展示这些临界边界。

图2-5　特征值临界面

在图2-6中，通过固定κ1的值来截取图2-5中的不同截面，从而探讨各个参数对于磨削稳定性的影响。在图2-6中可以看到，在无量纲磨削刚度比较小的时候（κ1=0.5），系统的稳定性区域（灰色）相对大得多。但随着κ1的增大，这些磨削稳定区域会被不稳定的区域（白色）逐渐蚕食掉，这意味着大的磨削刚度会降低磨削稳定性。另一方面，还可以看出两个时滞τg和τw也对磨削的稳定性有很大程度的影响，且这种影响随着时滞的改变呈现出了一种周期性。例如，从图2-6中可以看出，随着τw的改变，该磨削过程会在稳定和不稳定之间不断地切换。再考虑到这里的时滞分别反映了砂轮和工件的转速，可以知道加工过程中转速的选取需要根据实际的情况，而不是一味地增大或是减小。

图2-6　临界曲线、磨削稳定（灰色）与不稳定（白色）区域：（a）κ1=0.5，（b）κ1=0.6，（c）κ1=0.8，（d）κ1=1.0。

为了从另一个角度说明磨削力对系统稳定性的影响，可固定τg的值去研究κ1和τw对于磨削稳定性的影响，相应的截面图都绘制在了图2-7中。可以看到，图2-7类似于车削颤振中的“Lobes”图。而由图2-7可以看出，该磨削过程在κ1＜0.4的时候会始终保持稳定，无论τg和τw的值是多少。但随着κ1的增大，可用的工件转速（对应于τw）的选择范围则越来越小。由此可知，减小砂轮与工件之间的磨削刚度对于维持磨削加工的稳定性具有极其重要的意义。

通过分析系统特征值找到了该磨削过程的稳定性边界以后，可以区分磨削加工过程的稳定和不稳定区域。在实际的磨削加工过程中，应当尽量去利用磨削稳定性区域，避免加工过程中的颤振。下一章中将探讨当参数跨过稳定性边界进入不稳定区域的时候颤振的主要产生形式。

图2-7　临界曲线、磨削稳定（灰色）与不稳定（白色）区域