为了分析方程（2-11）的平衡点稳定性，需要讨论其特征值。首先，其特征矩阵为

相应的特征方程为

将方程（2-13）代入方程（2-14），得到

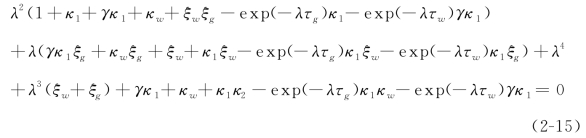
其中，λ=σ±iω 代表系统的特征值。当它具有正实部时（σ＞0），系统会失稳，并引发磨削颤振，因而该磨削过程稳定的前提是所有的特征值都具有负实部。对此，可以通过计算临界的情况（σ=0），在参数空间中区分出磨削过程稳定和不稳定的区域。

为了得到该稳定性边界，在方程（2-15）中考虑λ=±iω 并且分离其实部和虚部，可得到(www.daowen.com)

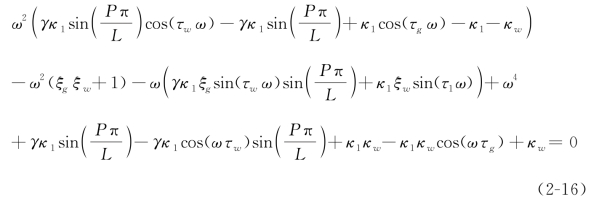
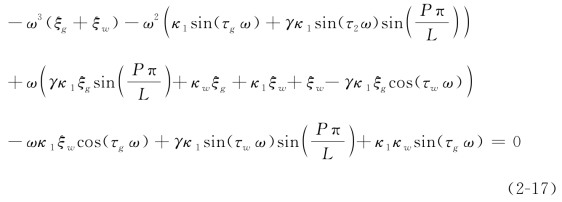
和可以看到，方程（2-16）和方程（2-17）是两个超越方程，且由于两个不同时滞τg和τw的存在，很难得到这两个方程的理论解。因此，在下面的分析中，将采用数值的办法连续地求解这两个方程。

为了同时求解方程（2-16）和方程（2-17），我们采用Newton-Raphson方法去得到数值的结果。众所周知，在初始值给得比较好的情况下，该数值方法具有极好的收敛性。然而其问题也在于，很多时候我们很难给出有效的初始值，从而得不到想要的数值结果。此外，在方程（2-16）和方程（2-17）中，我们需要求解的量包括磨削力参数κ1、τg和τw以及方程特征值ω，为了能够在三维参数空间中连续地找到系统的稳定性边界（即方程的解），必须始终给出有效的初始值。为此，给出了如图2-3中所描述的延拓算法[202]来达到该目的。

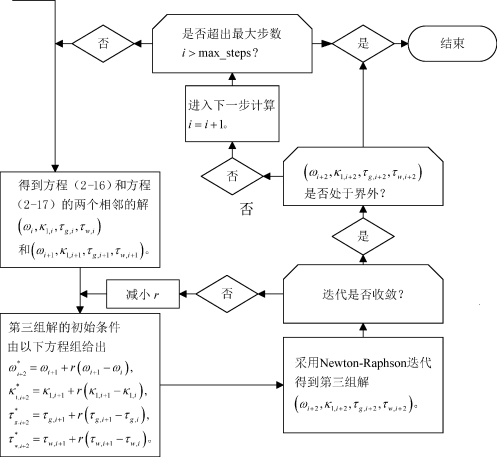
图2-3　延拓算法

采用图2-3中所描述的延拓算法，可以得到系统的稳定性边界线。即使是在三维的参数空间κ1-τg-τw中，通过改变延拓的方向进行多次计算，也能够在三维空间中得到稳定性边界面，用来区分磨削稳定和不稳定区域。下面就用一个算例来证实该算法的有效性。