图2-1描述了一个典型的切入式外圆磨削过程,在该过程中,高速旋转的砂轮被装在砂轮架上而低速旋转的工件则安装于两个尾架上,与此同时,砂轮架朝着工件的方向作缓慢的进给,从而保证磨削过程中的切削用量。从图2-1可以看出,砂轮被视为一个质量弹簧振子,它具有质量mg(kg)、刚度kg(N·m-1)、阻尼cg(N·s·m-1)、半径rg(m)和转速Ng(r·min-1)。同时,工件被看作一个简支于两个尾架上的Euler-Bernoulli梁,它具有密度ρ(kg·m-3)、弹性模量E(N·m-2)、阻尼Cw(N·s·m-2)、半径rw(m)和转速Nw(r·min-1)。为了描述该加工过程的动力学行为,我们将砂轮和工件的位移标记为Xg(m)和Xw(m),同时还考虑加工过程中砂轮的进给量f(m)。此外,考虑梁的连续体模型,其轴向的坐标记为S(m),砂轮处于位置P(m)而工件的总长为L(m)。
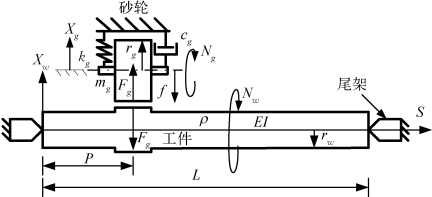
图2-1 切入式磨削加工示意图
当磨削一个细长的工件时,图2-1中的砂轮和工件的动力学方程中应考虑工件的几何非线性,即它们满足以下方程[210]:
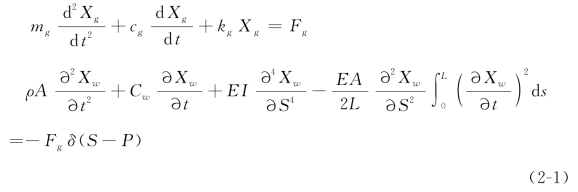
其中,![]() 。考虑到砂轮和工件的接触,公式(2-1)中的Dirac Delta函数δ(S-P)代表它们的接触位置。此外,考虑到工件被简支于两个尾架之间,其边界条件应为
。考虑到砂轮和工件的接触,公式(2-1)中的Dirac Delta函数δ(S-P)代表它们的接触位置。此外,考虑到工件被简支于两个尾架之间,其边界条件应为
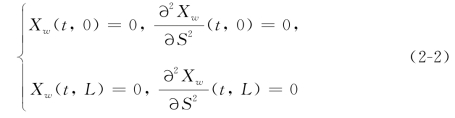
接下来需要说明的是砂轮和工件之间的法向磨削力Fg(N),它代表了砂轮和工件之间的相互作用且决定了整个磨削加工过程的动力学行为。根据Liu和Payre的模型[168],磨削力Fg应该与当前的磨削深度Dg(m)成正比,因此它们最简单的关系为
![]()
式中,kc为磨削刚度(N·m-1)。而根据Thompson的双再生模型可知,磨削深度Dg除了与图2-1中的进给量f 有关外,还与砂轮与工件的位置相关,这一点可以从图2-2中看出。在图2-1(a)中,Dg反映了工件和砂轮之间相互作用的深度,图2-1(b)则说明Dg包含了两部分,它们分别是砂轮切入工件的深度δw和工件切入砂轮的深度δg。从图2-1(b)中还可以看出,δw不仅包括当前的进给量f,还含有当前工件砂轮的相对位置Xg(t)-Xw(t,P),以及由再生效应引入的时滞项Xg(t-Tg)。与之相应,本书从同样的角度出发考虑δg,最终可以得到[168]
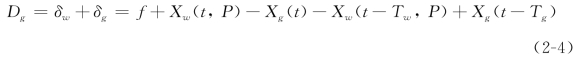 (https://www.daowen.com)
(https://www.daowen.com)
其中
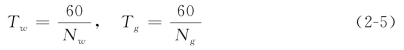
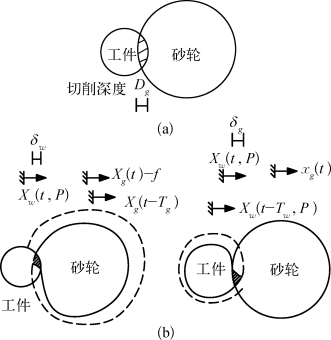
图2-2 切削深度
值得一提的是,公式(2-4)中的Tw(s)和Tg(s)分别代表了工件和砂轮的旋转周期。它们体现了切削加工过程中的再生效应,反映了切削深度不仅与当前状态有关,还和它们一个周期之前的状态相关。
然后,根据Liu所采用的线性磨削力公式(2-3),可以知道磨削力与工件和砂轮位移的关系为

考虑到工件的两端简支边界条件,可以将工件的位移Xw(t,S)展开为
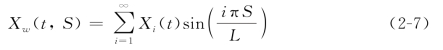
将公式(2-7)代入模型(2-1)并采用Galerkin截断的方法且仅保留工件的第一阶模态(i=1),可以得到简化后的磨削动力学模型为
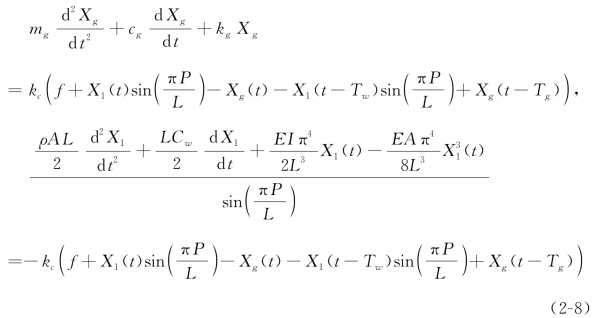
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







