前面已讨论了拉普拉斯变换在电路分析、传递函数和求解线性微积分方程方面的应用，除此以外，拉普拉斯变换在信号处理和控制系统等领域也有很多应用，下面简要介绍网络稳定性判别（Network Stability Criterion）和网络综合生成（Network Synthesis）。

当t→∞时，电路的冲激响应h（t）收敛到一个有限值，则该电路是稳定的，否则，电路就是不稳定的。电路稳定的数学表达式为　

因冲激响应h（t）的拉普拉斯变换是电路的网络函数H（s），而H（s）的一般表达式与极点关系为

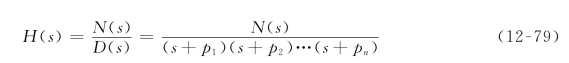
可见，若要电路稳定，则H（s）必须满足两个条件：第一，分子多项式N（s）的次数必须小于分母多项式D（s）的次数；否则为长除法，会得到

式（12-80）中的R（s）是长除法的余项，它的次数小于D（s）的次数，而这种情况下式（12-80）H（s）的逆变换不满足式（12-78）的稳定条件；第二，式（12-79）中H（s）的所有极点必须有负的实部，或者说，所有的极点都必须位于s平面的左半部。因为式（12-79）的拉普拉斯逆变换为

可见，要使随时间增加而减小，每个极点pi必须是正的，也就说极点s=-pi处于s平面的左半平面内。

一个电路，若只是由无源元件和独立电源构成的，则该电路是稳定的。如RLC串联电路，设激励源电压为US（s），若以电容两端电压UC（s）为响应，可以求得它的网络函数为

式（12-82）中，的特征根为

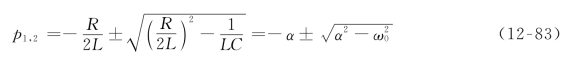
其中，。

因为R、L、C总是大于零的，所以两个极点处于s平面的左半部分，说明电路总是稳定的。若R=0，则α=0，电路成为不稳定的，但这种情况只有理论上的可能，是不会发生的，因为R总不可能真正为零。

若是有源电路，或是受控无源电路，就可能是非稳定的，因为它们有能量提供给电路元件。振荡器就是一个非稳定电路的典型例子，它的网络函数为

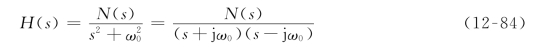
所以，振荡器的输出为正弦波。因此，可根据电路的网络函数H（s）就可以判断该电路是否稳定。

网络综合生成是给定网络函数，设计一个适当的电路网络满足该网络函数的过程。在网络分析技术中，是对给定的网络求其网络函数；而网络生成技术则是反过来，对给定的网络函数，求与其相应的电路网络。

要注意的是，网络分析的结果只有一个，而网络生成的答案却有许多不同的结果，也许没有结果，因为可以有多种电路来表示同一个网络函数的形式。

例12-27　确定使图12-21所示电路稳定的k值。

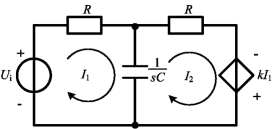
图12-21　例12-27图

解　应用网孔电流法，可得两个网孔分别得到：

整理得(www.daowen.com)

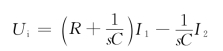
将上式写成矩阵形式

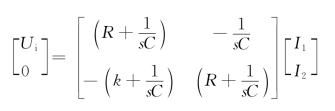
其行列式为

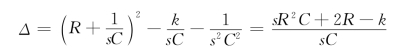
特征方程的根有一个极点为

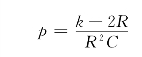
由此可得，当k＜2R时，极点p＜0；当k＞2R时，极点p＞0。所以，当k＜2R时，电路稳定；当k＞2R时，电路不稳定。电路稳定的条件为k＜2R。

例12-28　图12-22（a）所示电路，给定的网络函数H（s）为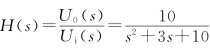，求电路中的L和C。

图12-22　例12-28图

解　图12-22（a）所示电路在s域中的等效电路如图12-22（b）所示。图中R和C并联等效阻抗为

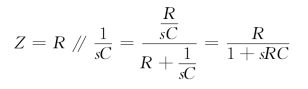
利用分压原理，有

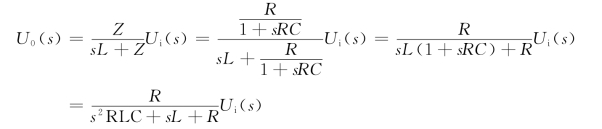
所以有

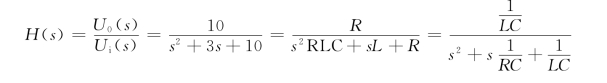
比较可得

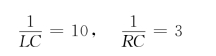
可见有许多不同的R、L、C能满足上述要求。所以，需要指定某个元件的值，才能确定另外两个元件的值。

若假设R=5Ω，则可求得

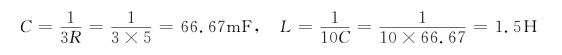
若假设R=1Ω，则可求得

一般将取R=1Ω的设计，认为是归一化的设计。