对于一个稳定的线性时不变零状态电路，当其激励是角频率为ω的正弦信号时，其网络函数为

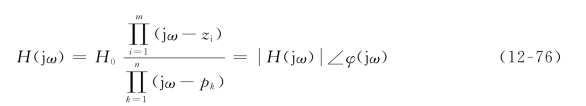
由式（12-76）可得幅频特性和相频特性分别为

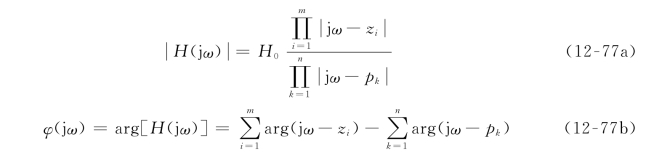
由式（12-77）可知，若一个电路的网络函数的零、极点已知，则利用该式可以计算出该电路的频率响应，同时也可以通过零、极点标示在s平面上用作图法定性地描绘出频率响应曲线。由此可见频率响应取决于网络函数的零、极点在s平面上的位置分布，而与比例因子H0无关。

总之，网络函数是一个重要的概念，从它的零、极点在s平面上的分布情况，可以预见电路时域响应的性质和频率特性；而且在给定激励下，通过网络函数，能确定网络的零状态响应和正弦稳态响应。对于稳态电路，可令s=jω，而由H（s）找到H（jω），便可以对电路进行频域分析。若给定正弦激励，则可求电路的正弦稳态响应；利用叠加原理还可以求非正弦周期信号作用下的稳态响应。

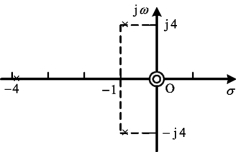
图12-20　例12-26图

例12-26　某电路的H（s）的零、极点分布如图12-20所示，且已知，0°＜argH（jω）＜90°。试求（1）；（2）当输入u1（t）=（1+sin4t）V时稳态响应u2（t）。

解　（1）由零、极点分成图可写出

由于，因此，有

即

(www.daowen.com)

（2）由于H（s）的极点均在s平面的左半开平面，所以电路是稳定的。即可用s=jω代入H（s）计算式中得到频域网络函数H（jω），即

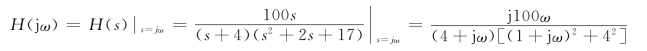
由于输入电压是非正弦信号，所以可用叠加原理来求响应。

若直流分量单独作用，即u1（0）=1V，ω=0，则有H（j0）=0，它所产生的响应为

所以，有u2（0）（t）=0

若正弦分量单独作用，即u1（1）=sin4tV，ω=4，则有

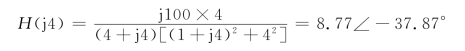
响应

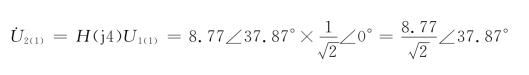
得

u2（1）（t）=8.77sin（4t-37.87°）V

所以对输入u1（t）的稳态响应u2（t）为

u2（t）=u2（0）（t）+u2（1）（t）=8.77sin（4t-37.87°）V