根据网络函数的定义可知,电路的零状态响应的象函数为
![]()
式(12-62)中![]() ,
,![]() ,而N(s)、D(s)、P(s)、Q(s)均为s的实系数多项式。D(s)Q(s)=0的根将包含D(s)=0的根和Q(s)=0的根,而Q(s)和D(s)的每个根(即R(s)的极点)都有一项与之相对应。因此,由部分分式法可知,R(s)可以展开为D(s)=0的根得出的各项与Q(s)=0的根得出的各项之和,对R(s)取拉氏变换可得电路零状态响应r(t)的时域形式,其中网络函数H(s)的极点(D(s)=0的根)相对应的所有项构成响应的自由分量或瞬态分量,它们仅与网络的结构和参数有关。激励函数E(s)的极点(Q(s)=0的根)相对应的所有项构成响应的强制分量,它不仅与网络的结构和参数有关,还与外施激励有关。例如,假设激励函数E(s)和网络函数H(s)的表示式分别为
,而N(s)、D(s)、P(s)、Q(s)均为s的实系数多项式。D(s)Q(s)=0的根将包含D(s)=0的根和Q(s)=0的根,而Q(s)和D(s)的每个根(即R(s)的极点)都有一项与之相对应。因此,由部分分式法可知,R(s)可以展开为D(s)=0的根得出的各项与Q(s)=0的根得出的各项之和,对R(s)取拉氏变换可得电路零状态响应r(t)的时域形式,其中网络函数H(s)的极点(D(s)=0的根)相对应的所有项构成响应的自由分量或瞬态分量,它们仅与网络的结构和参数有关。激励函数E(s)的极点(Q(s)=0的根)相对应的所有项构成响应的强制分量,它不仅与网络的结构和参数有关,还与外施激励有关。例如,假设激励函数E(s)和网络函数H(s)的表示式分别为

则有

假设式(12-63)中,n>m,v>q,分子与分母没有相同因式,且R(s)中不含重极点,则式(12-63)的部分分式展开式为

对式(12-64)取拉普拉斯逆变换可得零状态响应为

式(12-65)中第一项是D(s)=0的根对应的响应为自由分量,其中的每一项![]() 对应着网络函数H(s)的一个极点pj;第二项是Q(s)=0的根对应的响应为强制分量,其中的每一项
对应着网络函数H(s)的一个极点pj;第二项是Q(s)=0的根对应的响应为强制分量,其中的每一项![]() 对应着激励函数E(s)的一个极点pl。
对应着激励函数E(s)的一个极点pl。
由于网络函数H(s)与单位冲激响应h(t)是拉氏变换对,而网络函数只要用其比例因子、m个零点、n个极点就可以完整地加以描述了,因此,H(s)在s平面上零、极点的分布情况将决定电路的冲激响应的特性。
下面讨论当H(s)只具有一阶极点pj(j=1,2,…,n)时,极点在s平面上不同位置所对应冲激响应的波形。由网络函数的性质可知,电路的冲激响应和该电路相应的网络函数构成拉氏变换对,所以电路单位冲激响应为
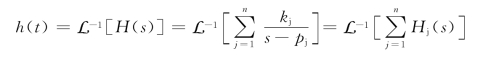

按部分分式展开法求式(12-66)中单位冲激响应第j项系数kj的计算公式为
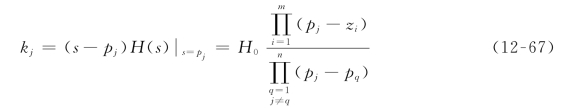
由式(12-67)可以看出,kj值不仅与极点pj相关,还与全部零点和极点值有关。因此,可以说,H(s)的极点确定冲激响应的波形,而零点只影响响应分量kj(j=1,2,…,n)的大小,它与极点共同决定冲激响应中每一项的量值kj(j=1,2,…,n)。因此,仅由H(s)的极点分布情况,便可完全预见冲激响应的h(t)形式。
(1)pj为实数,即H(s)的极点pj位于s平面的实轴上。根据式(12-66)可得对应的冲激响应分量hj(t)为(https://www.daowen.com)

由式(12-68)可知,当pj为负实根(位于负实轴)时,hj(t)随t按指数衰减;pj=0(位于原点)时,hj(t)为阶跃函数;当pj为正实根(位于正实轴)时,hj(t)随t按指数增长;![]() 越大,按指数衰减或增长的速度越快。这三种实数极点在s平面的分布及其对应冲激响应分量波形如图12-19(a)、图12-19(b)、图12-19(c)所示。
越大,按指数衰减或增长的速度越快。这三种实数极点在s平面的分布及其对应冲激响应分量波形如图12-19(a)、图12-19(b)、图12-19(c)所示。

图12-19 网络函数的一阶极点与冲激响应的关系
(2)pj为复数,由于复数极点是共轭出现的,故设pj=α+jω,![]() ,由式(12-68)中取出两个共轭项有
,由式(12-68)中取出两个共轭项有

式中,φ=argkj为展开系数kj的幅角。由此式可知,其对应冲激响应分量hj(j+1)(t)是以指数曲线为包络线的正弦函数。若共轭极点位于左半平面,则对应冲激响应分量为衰减振荡;若共轭极点位于右半平面,则对应冲激响应分量为增长振荡。这两共轭极点对应冲激响应分量波形如图12-19(d)、(e)所示。
(3)pj为纯虚数,即H(s)的极点pj位于s平面的虚轴上。同理可得
![]()
这种纯虚数共轭极点在s平面的分布及其对应冲激响应分量波形如图12-19(f)所示,为等幅正弦振荡,且![]() 越大,振荡频率越高。
越大,振荡频率越高。
综上所述,可得出H(s)的一阶极点pj(j=1,2,…,n)与冲激响应hj(t)的关系为:
①H(s)的所有极点位于s平面的左半平面,则h(t)波形随时间增长而衰减至零;
②H(s)的所有极点位于s平面的右半平面,则h(t)波形随时间增长而趋于无穷大;
③H(s)的所有极点位于s平面的虚轴上,则h(t)为阶跃函数(实极点位于原点)或等幅振荡(共轭极点)。
在电路理论中,按照h(t)随时间t增长衰减至零、趋于无穷大以及趋于一个非零数值或形成一个等幅振荡而将电路划分为稳定、不稳定与临界稳定三大类,而H(s)的极点分布决定h(t)的变化情况,因此,由H(s)的极点分布可以判断电路的稳定性:
若电路网络函数H(s)的所有极点位于s平面的左半平面(不包括虚轴),则有![]()
![]() ,电路稳定;
,电路稳定;
若电路网络函数H(s)的所有极点位于s平面的右半平面(不包括虚轴),或在虚轴上具有二阶或二阶以上的重极点,则![]() ,电路不稳定。
,电路不稳定。
若电路网络函数H(s)在s平面的虚轴上有s=0的单极点或一对共轭单极点,其余极点均位于s平面的左半平面,则经过足够长时间之后,h(t)趋于一个非零的数值或形成一个等幅振荡,电路属于临界稳定。由于临界稳定也属于稳定,所以可把稳定和临界稳定电路的单位冲激响应合而表示为
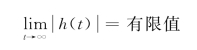
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







