网络函数一般是一个实系数有理式，即

式（12-61）中，ai（i=1，2，3，…，n）和bj（i=1，2，3，…，m）均为实系数；n和m为正整数，且n≥m；为一实常数，称为比例因子；zi（i=1，2，3，…，m）为N（s）=0的根，当s=zi时，H（s）=0，故zi（i=1，2，3，…，m）称为网络函数H（s）的零点；pj（j=1，2，3，…，n）为D（s）=0的根，当s=pj时，H（s）趋于无穷大，故pj（j=1，2，3，…，n）称为网络函数H（s）的极点。若N（s）和D（s）分别有重根，则分别称它们为网络函数H（s）的重零点和重极点。

由于N（s）和D（s）为实系数有理多项式，故其根即网络函数H（s）的零点和极点可能为实数、纯虚数或复数。若以复数s的实部σ为横轴，虚部jω为纵轴，就可得到一个复频域平面，称之为复平面或s平面。网络函数H（s）的零点在s平面上用小圆圈“○”表示，极点用小叉“×”表示，从而得到网络函数H（s）的零点、极点分布图，简称零极点图或称为极零点图。对于二重零点和二重极点分别用两个同心小圆圈“◎”和两划小叉“”表示，对于高阶重零点和重极点。依此类推。

由此可见，一个网络函数只要用其比例因子，m个零点、n个极点就可以完整地加以描述，因此，在描述电路特性方面，网络函数H（s）和零、极点图是等价的。

例12-25　图12-18（a）所示含理想运算放大器电路，已知uS（t）=2ε（t）V，试求电压转移函数，并在复平面上绘出其零、极点图。

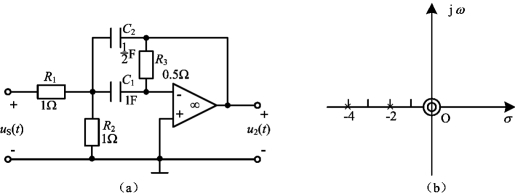
图12-18　例12-25图

解　由节点分析法有(www.daowen.com)

因为U-（s）=U+（s）=0，所以有

联立解得

代入已知参数，得

该函数的零点为：Z1=0；极点为：p1=-2，p2=-4。其零、极点图如图12-25（b）所示。