1.网络函数定义
在含有一个任意函数形式激励源的零状态线性时不变电路(如图12-14所示)中,若激励函数e(t)(可以是任意波形)的象函数为E(s),与该激励相应的零状态响应r(t)的象函数为R(s),则定义该网络的网络函数H(s)为

式中的网络函数H(s)是复频率s=σ+jω的函数,因而它比H(jω)有着更为丰富的内容。H(s)的定义域为复平面s,故而将任意输入与其零状态响应联系起来了,而H(jω)只是在正弦稳态输入下输出向量与输入向量之比。

图12-14 线性时不变电路中激励与零状态间的关系
(a)时域形式框图;(b)对应复频域形式框图
与正弦稳态下网络函数相类似,复频域的网络函数也分为驱动点函数与转移函数两大类,如果激励和响应属于同一端口,对应的网络函数则称为策动点函数,若激励与响应不属于同一端口,则称为转移函数或传递函数。由于激励和响应可以是电压也可以是电流,故网络函数可能是策动点阻抗、策动点导纳,或转移阻抗、转移导纳、转移电压比、转移电流比。电路网络函数的计算方法,也是依据具体电路的特点,选择网孔法、节点法或其他任意线性电路的分析方法。
2.网络函数的性质
(1)网络函数只与电路的结构参数有关,而与激励无关。
网络函数仅与电路的拓扑结构和元件参数有关,而与外加输入无关,即在任意波形的外加激励下,其零状态响应的象函数与输入的象函数的比值是一定的。这是因为在时域中,零状态响应与激励之间满足线性关系,因此它们的象函数之间也满足线性关系,即网络函数不随激励大小的变化而变化,只与网络的拓扑结构和元件的参数有关。当电路的拓扑结构和元件的参数确定以后,则相应的网络函数就确定了。所以,网络函数反映了电路的固有动态性能。因此,通过网络函数,在不求解电路的情况下,就可以定性地了解到该电路在过渡过程中的一些暂态特性。
(2)网络函数是复数量s的一个实系数有理式。
由于线性时不变电路中元件的参数为定值,故列出的复频域代数方程为s的实系数代数方程,因此,集总参数电路的网络函数一定是s的实系数有理函数,其分子、分母多项式的根为实数或共轭复数。
(3)网络函数是电路单位冲激响应的象函数
根据复频域的网络函数可以计算线性时不变电路的零状态响应。由式(12-56)可得R(s)=E(s)H(s),对其两边取拉普拉斯逆变换可得出
![]()
由此可知,只要求出线性时不变电路激励函数的拉氏变换E(s),并根据该电路的s域模型求出相应的网络函数H(s),就可以得出零状态响应的象函数R(s)=E(s)H(s)。由卷积定理有L[h(t)*e(t)]=E(s)H(s)。因此,这种方法的实质就是将在时域中用激励函数和冲激响应的卷积积分来求零状态响应置于s域中进行,其中H(s)不需要求出冲激响应h(t)再经拉氏变换求得,而是由s域电路直接求出。
若激励为冲激函数,即e(t)=δ(t),则其象函数为![]() ,由式(12-56)有
,由式(12-56)有

或
![]()
这表明电路的冲激响应和该电路相应的网络函数构成拉氏变换对。因此,对于任一线性时不变电路,可利用其复频域模型计算其网络函数,再作反变换即可得到相应的冲激响应。
(4)在一般情况下,网络函数分母多项式的根即为对应电路的固有频率。
由式(12-56)可得R(s)=E(s)H(s),由上面的讨论可知,这正是时域卷积积分在s域中的体现。通常H(s)和E(s)均为复频率s的有理分式,即
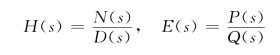
因而有
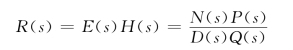
设D(s)和Q(s)具有单根,则
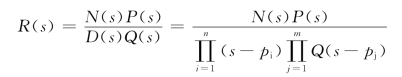
应用部分分式展开,得

则R(s)对应的象函数为

式(12-60)表明,网络的零状态响应由两部分组成,第一部分与网络函数分母D(s)的特征根有关,为响应中的自由分量;而第二部分则与网络激励有关,为响应中的强迫分量,所以,D(s)=0为电路方程对应的特征方程,pi(i=1,2,3,…,n)就是电路响应变量r(t)的固有频率(或自然频率)。因此,H(s)分母多项式的根即为对应电路变量的固有频率。
例12-22 求图12-15(a)所示电路的电压比![]() 及单位冲激响应。
及单位冲激响应。

图12-15 例12-22图
解 对电路去耦,其等效电路如图12-15(b)所示。于是有
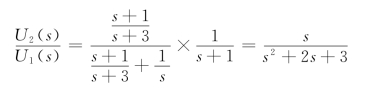
其单位冲激响应为


例12-23 已知图12-16(a)所示电路。
(1)求![]() ;
;
(2)若激励f(t)=cos2tε(t)V,欲使u2(t)中不出现强迫响应,试求LC的值;
(3)若R=1Ω,L=1H,试按第(2)问条件求u2(t)。

图12-16 例12-23图
解 (1)作图12-16(a)所示电路的复频域电路如图12-16(b)所示,由此可得(www.daowen.com)

所以

(2)激励源的象函数为:

故有

可见,若要使u2(t)中不出现强迫响应分量,则必须有H(s)的零点与F(s)的极点相互抵消,即有![]() ,故得
,故得![]() ,即LC=4。
,即LC=4。
(3)因L=1H,所以在(2)条件下,故得![]() ,此时
,此时

所以有
![]()
例12-24 图12-17为s域的电路图,求(1)传递函数![]() ;(2)冲激响应;(3)ui(t)=ε(t);(4)ui(t)=8cos2tV。
;(2)冲激响应;(3)ui(t)=ε(t);(4)ui(t)=8cos2tV。
解 (1)由图可得
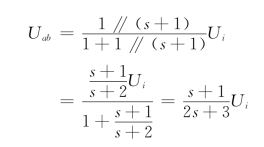

图12-17 例12-24图
由分压原理可得
![]()
联立上述两式可得
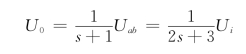
故有
![]()
(2)把H(s)改写成

由于H(s)的拉普拉斯逆变换就是时间中的冲激响应,因此
![]()
(3)若ui(t)=ε(t),由![]() ,于是有
,于是有

式中

所以在ui(t)=ε(t)时,有

其拉氏逆变换为

(4)若ui(t)=8cos2tV,则![]() ,于是有
,于是有

所以有

为求k2,k3采用代数法,将U0(s)的表达两边同时乘以![]() ,可得
,可得
![]()
整理得

比较两边的系数可得

所以,输入ui(t)=8cos2tV时,其输出为

其逆变换为

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







