相量分析法通过将正弦时间函数变换为对应的相量，从而把求解线性时不变动态电路的正弦稳态问题归结为以相量为变量的线性代数方程。与此类似，复频域分析法通过将时间函数变换为对应的象函数，从而把线性时不变电路的暂态过程的问题归结为求解以象函数为变量的线性代数方程。因此，利用拉氏变换法分析电路的暂态过程，又称为复频域分析法。复频域分析也有两种方法：一种方法是先列出所求线性时不变动态电路变量的常系数线性微分方程，再对方程进行拉氏变换从而把微分方程转换为复频域中的代数方程，解此代数方程求出待求响应的象函数并对其进行拉氏逆变换即可求得待求的时域响应。另一种方法是先将动态电路的时域模型转换为复频域模型，再根据复频域电路模型利用合适的电路分析方法列出响应变量象函数的方程，然后算出响应的象函数，最后经过逆变换得到复频域响应的原函数。本节讨论后一种分析方法。

复频域分析法和相量法的基本思想类似，仿照相量分析法，复频域分析法的一般步骤为：

（1）根据换路前一瞬间的时域电路模型，计算所有电压电流和电容电压在该时间的值，如若电路在t=0时发生换路，则应求出iL（0-）和uC（0-）的值，以便确定电路的复频域模型中的附加电源；

（2）根据电路的时域模型画出其对应的复频域模型，即画出运算电路；

（3）应用复频域形式的KVL、KCL和元件的伏安关系、等效变换以及电路定理等电阻电路分析法，建立电路的复频域的节点方程或回路方程，用复数运算法则求解方程，求响应的象函数；

（4）将响应的象函数部分分式展开；

（5）通过拉氏逆变换求得响应的时域形式。

例12-14　电路如图12-6（a）所示，电路原来处于稳定状态，t=0时开关S断开，求电感电流iL（t）。

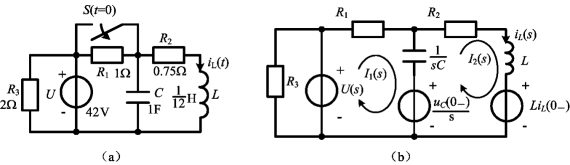
图12-6　例12-14图

解　当t＜0时，，uC（0-）=U=42V，当t＞0时，其复频域电路如图12-6（b）所示。

应用回路分析法，有

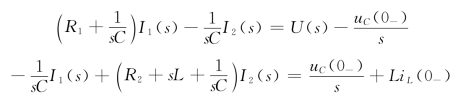
代入数据，求得

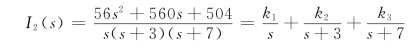
应用部分分式展开法，得

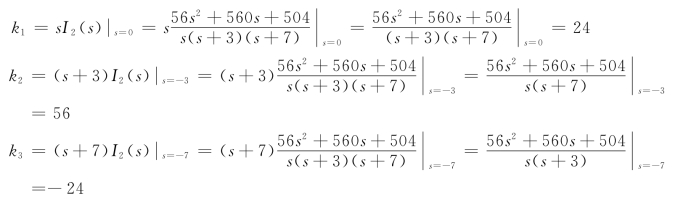
所以有

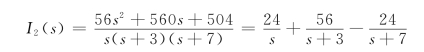
通过拉氏逆变换，得

iL（t）=i2（t）=（24+56e-3t-24e-7t）A t≥0

例12-15　求图12-7（a）所示电路的零状态响应i1（t）和i2（t）。

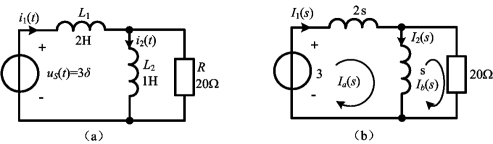
图12-7　例12-15图

解　由于电路处于零状态，故有i1（0-）=i2（0-）=0，复频域电路如图12-7（b）所示。设两网孔电流分别为Ia（s）和Ib（s），其绕向均为顺时钟方向，则网孔电流方程为

（s+2s）Ia（s）-sIb（s）=3

-sIa（s）+（s+20）Ib（s）=0

解之得

通过拉氏逆变换，得

ia（t）=（1+0.5e-30t）A， ib（t）=1.5e-30tA

则有

i1（t）=ia（t）=（1+0.5e-30t）A

i1（t）=ia（t）-ib（t）=（1+0.5e-30t）-1.5e-30t=（1-e-30t）A

例12-16　图12-8（a）所示电路，在开关S闭合前已处于稳态，试求t＞0时的电感电压uL（t）。

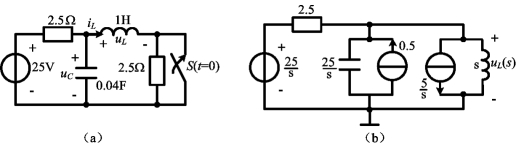
图12-8　例12-16图

解　t=0-时，电路处于直流稳态，电感短路，电容开路，所以，有

运算电路如图12-8（b）所示。设接地点为参考节点，利用节点分析法得

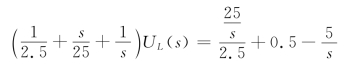
整理得

（s2+10s+25）UL（s）=12.5s+125

所以，有

取上式的拉氏逆变换得

uL（t）=（62.5t+12.5）e-5t=12.5（5t+1）e-5tV

例12-17　电路图12-9（a）所示，已知uS（t）=2[ε（t）-ε（t-1）]V，uC（0-）=1V，iL（0-）=2A。求t≥0时的电容电压uC（t）。

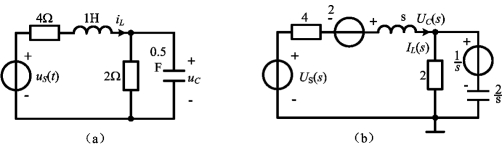
图12-9　例12-17图(www.daowen.com)

解　电源的象函数为

运算电路如图12-9（b）所示。节点电压方程为

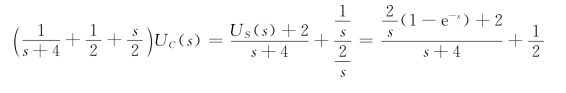
所以

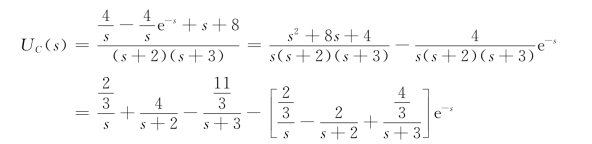
取拉普拉斯逆变换，得

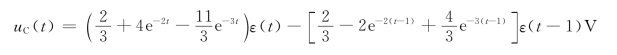
例12-18　图12-10（a）所示电路中，已知US=10V，R1=R2=2Ω，L=2H，C=2F，r=5Ω。在电路达到稳态时开关S合上，求流经开关S的电流。

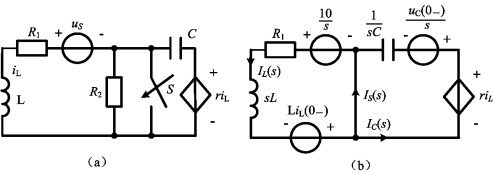
图12-10　例12-18图

解　设t=0时开关S合上，t=0-时为直流稳态，电感短路，电容开路。由此可求出

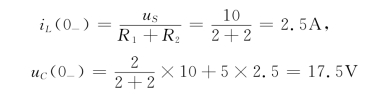
作t＞0的运算电路如图12-10（b）所示，由此可得

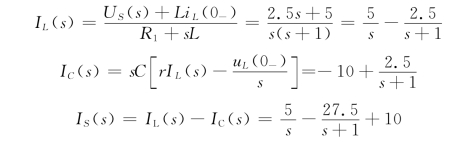
则流经开关S的电流为

例12-19　图12-11（a）所示电路中，已知R1=3Ω，R2=2Ω，L1=0.3H，L2=0.5H，C=1F，M=0.1H，uS=[30ε（-t）+15ε（t）]V。求t＞0时的电流i（t）。

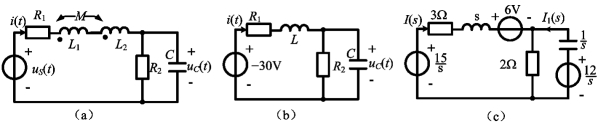
图12-11　例12-19图

解　由于两电感顺向串联，其等效为一个电感：，t=0-时的电路如图12-11（b）所示，有，uC（0-）=-6×2=-12V。作t＞0时的运算电路如图12-11（c）所示，由此可得回路电流方程为

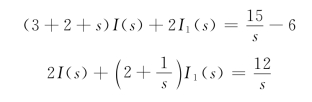
解得：

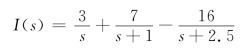
取拉普拉斯逆变换，得

i（t）=[3+7e-t-16e-2.5t]A t≥0

例12-20　图12-12（a）所示电路，当t＜0时，开关S打开，电路已稳定；当t=0时，闭合开关S。求当t＞0时的全响应i2（t）。

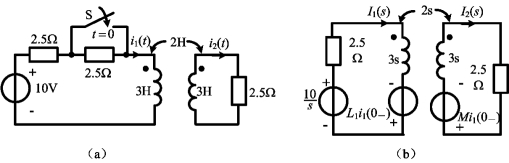
图12-12　例12-20图

解　因当t＜0时，开关S打开，电路已稳定，故根据图12-12（a）可得

当t＞0时，复频域电路如12-12（b）所示。于是以I1（s）和I2（s）为变量对两网孔列KVL方程为

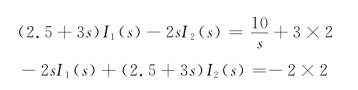
解得

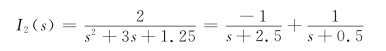
取拉普拉斯逆变换，得

i2（t）=（-e-2.5t+e-0.5t）ε（t）A t≥0

该题也可以采用去耦等效电路进行分析，其结果与直接分析相同。

例12-21　图12-13（a）所示电路，已知R1=R2=1Ω，L1=L2=1H，回转电阻r=1Ω，求。

解　将图12-13（a）所示电路用图12-13（b）所示电路来等效，其中，，其复频域电路如图12-13（c）所示。用节点分析法，有

图12-13　例12-21图

解得

所以，有

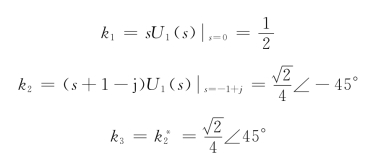
所以

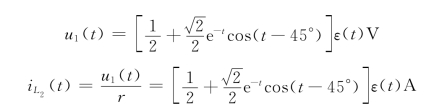
该也可以将回转器用受控源模型代替，然后按含有受控源的电路进行分析。