在利用拉普拉斯变换求得线性时不变动态电路暂态响应的拉氏变换式之后,为了得到其对应的时域响应,需要对响应进行拉普拉斯逆变换。
若已知F(s),则可以求出它对应的原函数f(t),这种运算称为拉普拉斯逆变换(简称拉氏逆变换)或拉普拉斯反变换(TheInverseLaplaceTransform),其定义为
![]()
式(12-18)可用算符![]() 简记为
简记为![]() 。
。
求拉氏逆变换可以用其定义式(12-18)直接计算,但需要按围线积分和留数定理计算复变函数的积分,比较困难,所以一般避开式(12-18)的直接计算。而是参照常用时间函数及其象函数表(如表12-1所示)的拉普拉斯变换来求得对应的原函数f(t)。由拉氏变换的微分性质和积分性质可知,其变换式中或者包含s或包含s-1,因此,由线性时不变动态电路导出的响应变量f(t)的拉氏变换F(s)通常可以表示为两个实系数的s的多项式之比,即s的一个有理分式,也称为s的有理函数,一般表示为

式中,N(s)是分子多项式,D(s)是分母多项式。N(s)=0的根称为F(s)的零点(Zero),而D(s)=0的根称为F(s)的极点(Pole)。虽然式(12-19)与式(7-5)的形式一样,但这里的F(s)是函数的拉普拉斯变换,并不一定是传递函数。用有理分式展开的方法将F(s)分解为一些简单项,它们的逆变换可以由表12-1查到。由此,要得到F(s)的拉氏逆变换包括以下步骤:
(1)用有理分式展开方法分解F(s)为若干简单项;
(2)对照表12-1查到每项对应的逆变换函数。
下面分析F(s)的三种可能形式及其拉氏逆变换的求法。
1.简单极点形式
设在D(s)=0的根中,有n个实数单根,分别为p1,p2,…,pn,则F(s)可以表示为

式中,p1,p2,…,pn,是各不相同的简单极点,且均不为D(s)=0的根。假设分子多项N(s)的次方数小于分母D(s)的次方数,用部分分式展开法把式(12-20)的F(s)分解为
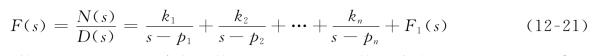
上式中展开系数k1,k2,…,kn为待定系数,称为F(s)的留数。将式(12-21)两边同乘以(s-p1),得到
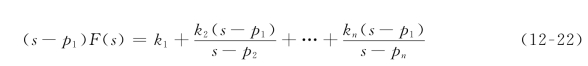
因为si≠pj,令式(12-22)中的s=p1,则有等式的右边只剩下k1项,所以有
![]()
一般情况下,有
![]()
上式称之为海维赛德定理(Heaviside's Theorem)。ki值已知后,代入式(12-21),由表12-1和式(12-21)中每一项的逆变换形式:

所以有
![]()
例12-11 求![]() 对应的原函数f(t)
对应的原函数f(t)
解 极点为P1=0,P2=-2,P3=-3,可令展开式为
![]()
根据留数法有
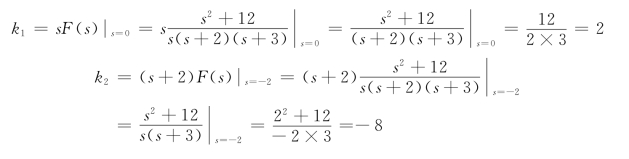
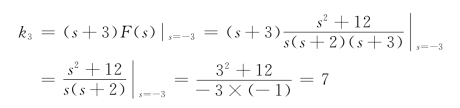
所以有
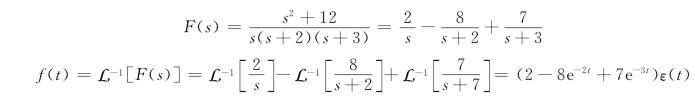
2.重复极点形式
假设F(s)在s=p1处有n个重复极点,则F(s)可改写为
![]()
式(12-27)中F1(s)是F(s)的余部,它在s=p1没有极点。待定系数确定如下:
对式(12-27)中的每一项都乘以(s-p)n,则将待定系数k1n单独分离出来,则有
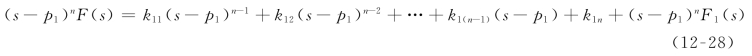
在式(12-28)中令s=p1,可求出k1n为
![]()
要确定展开系数k1(n-1),对式(12-28)中的每一项对s求一阶导数,免去了k1n,将k1(n-1)单独分离出来,即有(https://www.daowen.com)
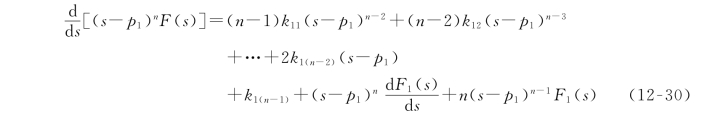
在上式中令s=p1,则可求出k1(n-1)为
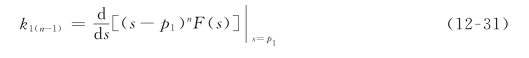
重复上述过程,有
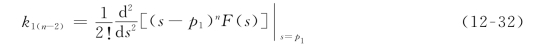
第m项系数为

式中,m=1,2,…,n-1。
随着m的增加,高阶微分的处理也较为困难,用这种部分分式展开法得到了后,式(12-27)右边的每一项都用其逆变换形式

所以有
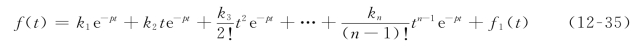
例12-12 求![]() 对应的原函数f(t)
对应的原函数f(t)
解 令s(s+1)3=0,得极点p1=0为单根,p2,3,4=-1为三重根,故F(s)的部分展开式为

其中,各系数确定如下
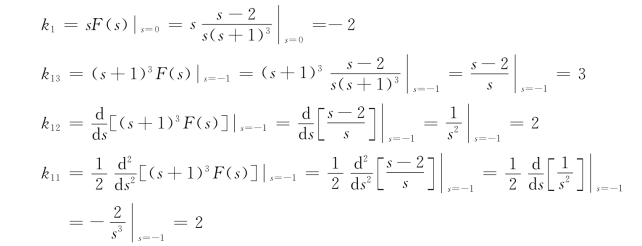
于是,得到
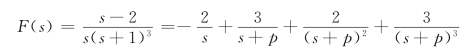
根据表12-1可知![]() ,所以有
,所以有
![]()
3.共轭复极点形式
由于实系数多项式的复根总是以共轭对出现的,故可设D(s)=0的根中含有一对共轭复根p1=α+jω,p2=α-jω,则F(s)可表示为
![]()
由于p1=α+jω,p2=α-jω均不为D1(s)=0的根,故上式可以展开如下形式的部分分式:
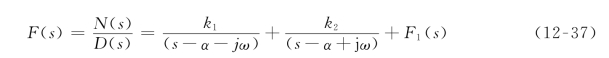
式(12-37)中的待定系数可由处理简单实极点的方法来处理,即
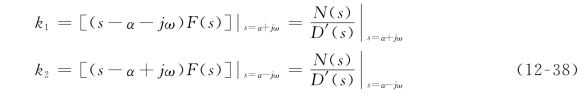
由于F(s)是实系数有理多项式之比,故k1、k2应为共轭复数。设![]() ,则
,则![]()
![]() ,因此,这两项部分分式对应的拉普拉斯逆变换为
,因此,这两项部分分式对应的拉普拉斯逆变换为
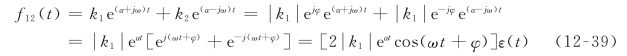
故式(12-37)对应的拉普拉斯逆变换为
![]()
例12-13 求 对应的原函数f(t)
对应的原函数f(t)
解 D(s)=(s+2)(s2+2s+2)=(s+2)(s+1+j1)(s+1-j1)=0的根为
p1=-2, p2=-1-j1, p3=-1+j1
故F(s)的部分分式可以表示为
![]()
其中,待定系数确定如下:
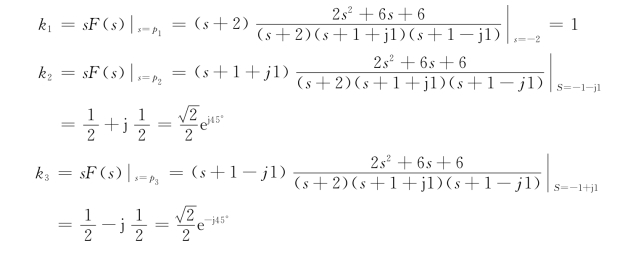
故有
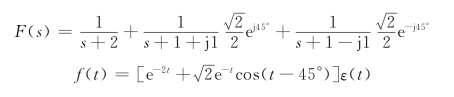
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





