1.线性性质

若F1（s）和F2（s）分别是时间函数f1（t）和f2（t）的拉普拉斯变换式，则对于任意实常数α和β，

证明：由拉普拉斯变换定义可得

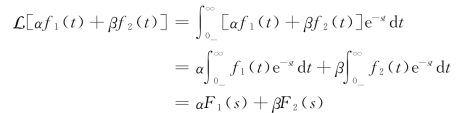
例12-2　求下列原函数的象函数。

（1）f（t）=cosωt；（2）f（t）=sinωt；（3）f（t）=K（1-e-at）

解　因为，

（1）由拉普拉斯变换的定义和线性性质，有

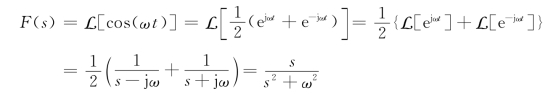
（2）

（3）

2.比例性质

若f（t）的拉普拉斯变换式为F（s），对于任意正常数a，则有

证明：由拉普拉斯变换定义可得：，

若令x=at，则，代入上式中，有

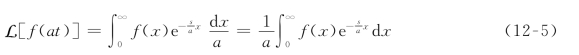
与拉普拉斯变换定义式（12-1）比较，可得

例12-3　求原函数sin2ωt的象函数。

解　因为，由比例性质有

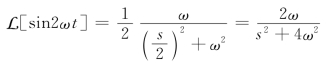
3.时域平移性质（延时性质）

若，则对任意正实数t0，有

证明：

令τ=t-t0，则上式可与成

时域平移性质表明，时间函数在时域中延迟t0，其象函数应乘以，称为时移因子。

例12-4　求原函数f（t）=ε（t）-ε（t-τ）的象函数。

解　因为，根据延迟性质，有

又根据拉普拉斯变换的线性性质，得

4.复频域平移性质

若，对于任意实数或复数s0，有

证明：由拉普拉斯变换定义式，有

式（12-7）表明，时间函数乘以，相当于其对应的象函数在s域内平移s0。也就是说的拉普拉斯变换可以由f（t）的拉普拉斯变换式得到，只要把其中的每个s都以s-s0取代即可，这就是复频域平移性质或称频率转移性质。

例12-5　求原函数f1（t）=e-atcosωt和f2（t）=e-atsinωt的象函数。

解　因为，利用复频域平移性质，有

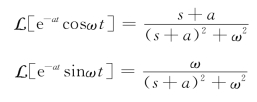
5.原函数微分性质

若，则f（t）对t的导数的拉普拉斯变换为

证明：由拉普拉斯变换定义，有

设u=e-st，f′（t）dt=v，则du=-se-st，dv=f（t）。又由于，所以有

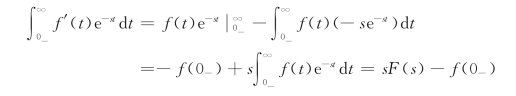
f（t）二阶导数的拉普拉斯变换，可以重复应用一阶导数的拉普拉斯变换得到

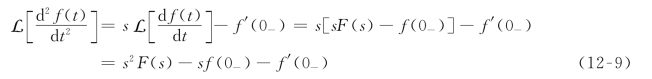
重复这种方法，可得到f（t）n阶导数的拉普拉斯变换为

例12-6　应用微分性质求原函数f1（t）=cosωt和f2（t）=δ（t）的象函数。

解　因为，而，所以有

又由于，而，所以有

6.复频率域微分性质

若，则有

证明：拉普拉斯变换定义有，两边对s求导

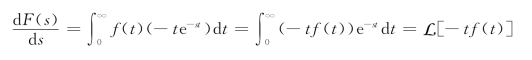
故有

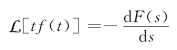
重复应用上述性质，导致如下结果

例12-7　利用复频域微分性质求原函数f（t）=te-at的象函数。(www.daowen.com)

解　因为，由复频率域微分性质可得

若a=0，则有

7.原函数积分性质

若，则f（t）对t的积分的拉普拉斯变换为

证明：令，，则，利用分部积分公式

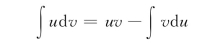
所以有

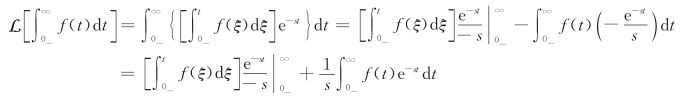
上式中等号右边的第一项，由于e-st在t→∞时为零，且在t=0时也为零，所以第一项为零，则有

例12-8　利用积分性质求原函数f（t）=t的象函数。

解　由于，所以有

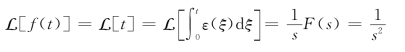
同理可求得

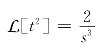
重复应用上式，则有

8.初值定理和终值定理

（1）初值定理

若函数f（t）及其导数的拉普拉斯变换存在，并且，则有

证明：由微分性质可知

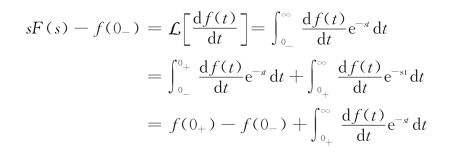
所以，有

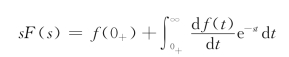
当s→∞时，上式右边第二项的极限为

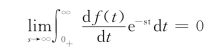
于是有

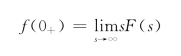
（2）终值定理

若函数f（t）及其导数的拉普拉斯变换存在，并且存在，则有

证明：由微分性质可知

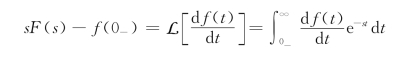
又

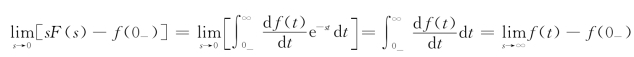
所以，有

由上面讨论可知，初值定理和终值定理允许由f（t）的拉普拉斯变换式F（s）直接求得f（t）的初值f（0）和其终值f（∞）。初值定理和终值定理建立了复频域与时域中起点和无穷远点之间的关系，由此也可检验拉普拉斯变换的正确性。但要注意的是，终值定理成立的条件是F（s）所有的极点必须落在s平面的左半平面内，即极点必须有负的实部。

例12-9　已知象函数为，试求原函数的初值和终值。

解　用初值定理

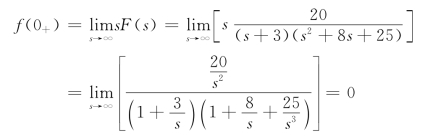
由于F（s）的极点是s=-3，-4±j3，这些极点都有负的实部，即都位于s平面的左半部，所以满足终值定理的使用条件，有

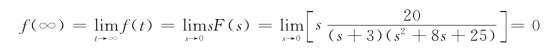
9.时域卷积定理

若，，则

证明：由卷积定义可得

在上式中交换积分次序并作变量代换x=t-ξ可得

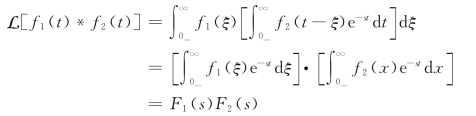
该性质表明，通过拉普拉斯变换，可将时域的卷积运算转化为复频域的乘法运算。这一结论常概括为：时域卷积，频域相乘。

例12-10　设f1（t）=5e-2t，f2（t）=2e-5t，f（t）=f1（t）*f1（t），（t为纯数），分别求对应的象函数F1（s）、F2（s）、F（s），验证卷积定理。

解　由拉普拉斯变换定义式，有

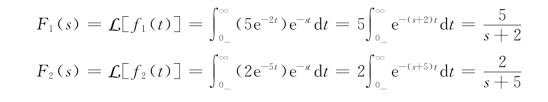
所以

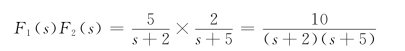
f1（t）和f2（t）的卷积为

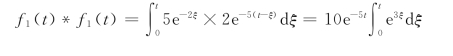
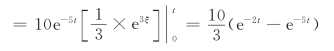
对上式取拉普拉斯变换得

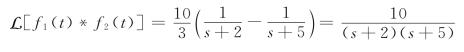
由此验证

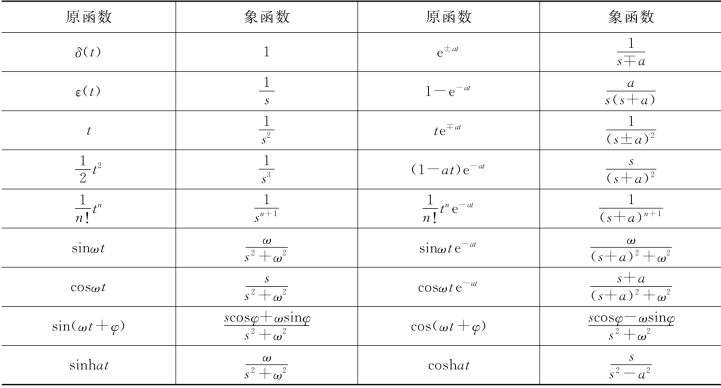
表12-1给出了一些常用的时间函数的象函数，供读者查阅。

表12-1　几种常用时间函数及其象函数