一阶非线性动态自治电路的分段线性化分析法与非线性电阻电路的分段线性化方法的思路相似，它也是将非线性电路的分析转化为线性电路和计算，即是根据非线性元件在电路动态变化过程中的“动态路径”画出其相应的线性等效电路。因此确定非线性元件的“动态路径”是分段线性化方法求解一阶非线性动态自治电路的关键，而所谓“动态路径”是指电路中的变量在非线性特性曲线上演变的点所移动的“方向”和“路径”。

图11-30（a）所示的一阶非线性自治电路中，电容C是线性的，含有非线性电阻性一端口电路N的DP图可用分段线性化曲线表示，如图11-30（b）所示。对于图11-30（a）所示的电路应用KCL和KVL，有i=-iC，u=uC，因此，一端口电路N的端口电压u和电流i在任一时刻，除了必须位于它的DP图上外，还应满足

我们把满足式（11-33）的电压u和电流i在DP图上移动的方向和路径称这它们的“动态路径”。一旦确定了“动态路径”，即可根据动态点在DP图所处的位置，由对应的折线段作出等效的线性电路，如果电容的初始状态已知，则可以用分段线性化法求出换路后电容电压变化的规律。

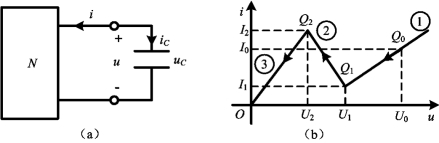
图11-30　一阶非线性自治电路及动态路径

首先确定“动态路径”。设图11-30（a）中电容的初始状态为已知值uC（0+）=U0。由于uC（t）=u（t），故有u（0+）=uC（0+）=U0，所以动态路径的初始点Q0（U0，I0）位于DP图第一折线段上。由于在P0点有i＞0，故有，这说明电压u在Q0点是减小的变化趋势。动态点在DP图上只能沿折线段①向左移动，如图11-30（b）中箭头所示。当动态点移到点Q1（U1，I1），将进入第二折线段②，在线段②内，仍有i＞0，，因而电压u继续减小，动态点在DP图上沿折线段②向左移动，当动态点移到点Q2（U2，I2），将进入第三折线段③，在线段③内，仍有i＞0，，所以动态点在DP图上沿折线段③向左移动到原点。在原点处，i=0，电压不再变化，即动态点停止于原点，因此，原点又称为平衡点，电容处于平衡状态，电路就工作在该点处，从暂态进入了稳态。可见，在给定的初始条件下，如图11-30（b）所示的电路动态点Q（u，i）的动态路径为Q0（U0，I0）→Q1（U1，I1）→Q2（U2，I2）→O（0，0）。

在确定“动态路径”后，根据DP图分段线性化的特点，在动态路径的每一折线段上，电路就转化成了一个一阶线性电路，应用一阶线性电路的分析方法可得解析解，从而获得电路的全局解。具体步骤如下

设DP图的第一折线段的表达式为u=R1i+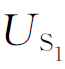，由此可以作出工作在第一折线段内的等效电路，如图11-31（a）所示。这是一个典型的全响应RC一阶电路，可直接应用三要素法求得其解为

式（11-34）中的t1是动态点到达Q1点的时刻，亦即离开折线段①进入折线段②的时刻。由于该时刻有uC（t1）=U1，故由式（11-33）可求出

设DP图的第二折线段的表达式为，由此可以作出工作在折线段③内的等效电路，如图11-31（b）所示。这也是一个典型的全响应RC一阶电路，同理可求得其解为

式（11-35）中的t2是动态点到达Q2点的时刻，由于该时刻有uC（t2）=U2，故可由式（11-34）求出

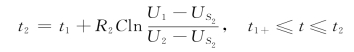
设DP图的第三折线段的表达式为u=R3i，由此可以作出工作在折线段②内的等效电路，如图11-31（c）所示。这是一个典型的零输入RC一阶电路，同理可求得其解为

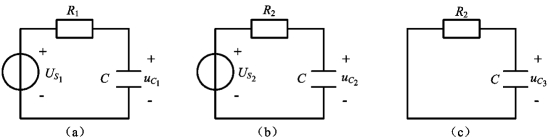
图11-31　图11-30（a）所示一阶非线性自治电路的分段等效电路

（a）工作在折线①上的等效电路；（b）工作在折线②上的等效电路；（c）工作在折线③上的等效电路

例11-15　一阶非线性电路如图11-32（a）所示，其中非线性电阻的DP图如图11-32（b）所示，讨论其充放电过程。

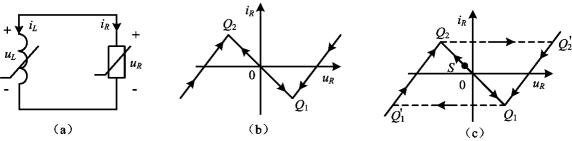
图11-32　例11-15图

解　由图11-32（a）所示电路，可知

所以有

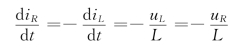
由于L＞0，所以有，当uR＞0时，有，因此，当电路的初始状态位于u～i平面的右半平面时，动态路径将从初始位置向下移动，即向着Q1方向移动；当uR＜0时，有。当电路的初始状态位于u～i平面的左半平面时，动态路径将从初始位置向上移动，即向着Q2方向移动，如图11-32（b）所示。当到达Q1或Q2点时，由于，故Q1和Q2不对应电路的最终稳定工作状态，iR将继续变化。若动态路径仍沿着DP图前进，将会违背约束。由于电感电流不能跃变，为寻求新的出路，这样就迫使电路的工作状态从Q1（或Q2）点瞬时跃变到Q′1（或Q′2），电感的电压发生了瞬时跳跃，这种现象称之为跳跃现象。假设初始状态位于DP图上的S，则整个动态路径如图11-32（c）所示，它构成一个闭合的路径，这说明电路的电压和电流从初始状态开始经过一段时间后，将进入周期性的振荡，振荡周期等于从Q′1到Q2和从Q′2到Q1的时间之和。

由于这种电路能产生周期性的电压和电流，所以，它具有振荡器的作用，但它所产生的电压和电流波形与正弦波相关很大，故把它称之为张驰振荡，对应于电感储存和释放能量的过程。同理，对于RC非线性电路也具有类似的张驰振荡，它对应于电容储存和释放能量的过程。

例11-16　在如图11-33（a）所示电路中，线性电容通过非线性电阻放电，非线性电阻伏安特性如图11-33（b）所示，已知C=1F，uC（0-）=3V，试求电容电压uC。

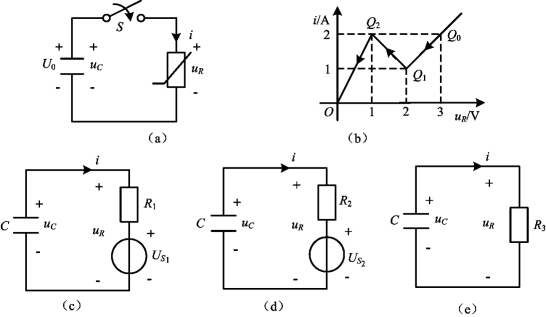
图11-33　例11-16图

解　此为分段线性RC电路的零输入响应问题。当关S闭合后电路方程为(www.daowen.com)

而uR=uC，故有

可见为电容的放电，从uC（0+）=uC（0-）=3V，直至衰减到零。因此，动态路径从Q0点起始，将沿着uR～i曲线从Q0经过Q1点和Q2点然后到O点，即动态路径为Q0→Q1→Q2→O。

（1）由图11-33（b）可知，在Q0Q1段，当从Q0点到Q1时，对应的uR从3V降到2V，即有

Q0（3V，2A）→Q1（2V，1A），所以有

因此有，R1=1Ω。其等效电路如图11-33（c）所示。根据三要素法可求得对应于图11-33（c）所示电路的解为

其中，τ1=R1C=1×1=1s。

设当从Q0点到Q1所需要的时间为t1，则有

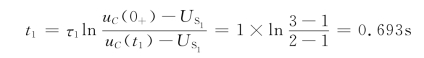
故有

（2）由图11-33（b）可知，在Q1Q2段，Q1（2V，1A）→Q2（1V，2A），所以有

则有：R2=-1Ω，。其等效电路如图11-33（d）所示。根据三要素法可求得对应于图11-33（d）所示电路的解为

其中，τ2=R2C=-1×1=-1s。

设当从Q1点到Q2所需要的时间为t2，则有

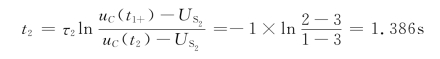
故有

（3）由图11-33（b）可知，在Q2O段，→Q2（1V，2A）→O（0，0），所以有

则有：。其等效电路如图11-33（e）所示。可求得对应于图11-33（e）所示电路的解为

其中，。所以有

综上可得电容电压在开关S闭合后的变化规律为

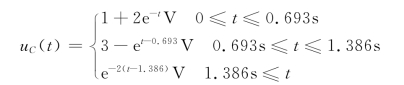
综上所述，非线性动态电路分段线性分析法与非线性直流电路的分段线性分析法的基本思想是一致的，但由于在动态电路中，响应是随时间变化的，在整个暂态过程中，响应可能要处于折线的不同分段处，因此求解方法有所不同，对于一阶非线性电路，其分析的一般步骤如下：

（1）用表示非线性元件的变量列写方程，根据此方程，确定非线性的变量在折线上移动的路径，包括起始段和后续各段，以及移动方向等；

（2）画出动态路径各折线段所对应的等效电路，并应用一阶线性电路的分析方法进行求解。