若方程右端函数项不显含时间变量t，则状态方程的标准形式为
式中，
为n维状态变量的列向量，它对应于n个独立的动态元件；F（x）为x的某种非线性函数向量。在电路理论中，凡电路元件参数随时间变化和有参数随时间变化的激励的电路的状态方程都是非自治方程；凡电路元件参数不随时间变化，在恒定激励或零输入情况下电路的状态方程都是自治方程。式（11-31）称为非自治方程，其对应的电路为非自治电路（Nonautonomous Circuit）。式（11-32）称为自治方程，其对应的电路称为自治电路（Autonomous Circuit）。
非线性动态电路的状态变量可以选电容的电压uC或电荷qC，也可以选电感的电流iL或磁链ψL，但由于非线性电容和非线性电感不能像线性元件一样用一个参数表示，因此，状态变量的选取有其特殊性，取决于非线性元件的性质。通常是根据元件特性方程的具体情况来选择状态变量，一般都是选控制变量作为状态变量的。具体来说，对于电感，若电感元件是电流控制型的，即电感的特性是电流控制的ψ～i曲线，则选电感的电流iL作为状态变量，若电感的特性是磁链控制的ψ～i曲线，则选电感的磁链ψL作为状态变量；对于电容，若电容元件是电压控制型的，即电容特性是电压控制的q～u曲线，则选电压uC作为状态变量，若电容特性是电荷控制的q～u曲线，则选电荷qC作为状态变量；而对于特性曲线是严格单调的电容和电感，其状态变量的选取没有限制，但从计算的观点来看，选择电容电荷qC和电感的磁链ψL作为状态变量是有利的。
2.状态方程的建立
非线性状态电路的状态方程的建立与线性电路类似，也可以采用观察法和系统法。由于非线性电路一般比较复杂，因而无法找到一种具有普适性的方法，只能根据具体电路选用合适的方法来建立其状态方程。这里只简要地介绍观察法建立非线性电路的状态方程。
观察法直接应用KVL、KCL和VAR来建立电路的状态方程，因此，它仅适用于结构简单的电路。
例11-13 非线性电路如图11-28所示，其中，电阻是流控的：
，
；电感是磁控的：
，
；电容是荷控的：
。试列写出该电路的状态方程。
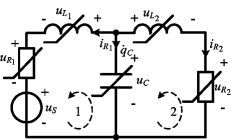
图11-28 例11-13图
解 因为非线性电感是磁控的，所以选磁链
、
为状态变量，而电容是荷控的，所以qC为状态变量。对节点①应用KCL有(www.daowen.com)
对回路1和回路2应用KVL有
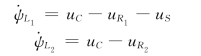
联立求解以上3式，并将元件的特性代入并整理得
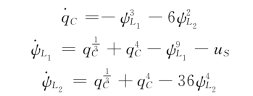
也可以用电源替代法来建立非线性动态电路的状态方程，就是将原电路中的电容元件和电感元件分别用电压为uC的电压源和电流为iL的电流源替代，这里的uC为电容元件两端的电压，iL流过为电感元件的电流，然后用叠加原理或其他合适的电路分析方法在替代后的电路中求解出电容支路的电流iC和电感支路的电压uL的表示式，最后应用
和
代入所求出的iC和uL的表示式中得出状态方程。
例11-14 电路如图11-29（a）所示，其中，R1=R2=R3=1Ω，uC=q3，iL=ψ3，试列写出该电路的状态方程。
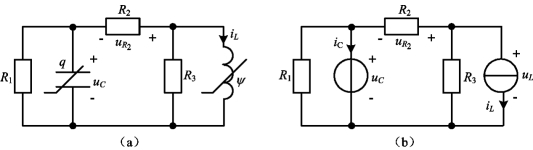
图11-29 例11-14图
解 用电压为uC的电压源代替电容，用电流为iC的电流源替代电感，得到图11-29（b）所示的等效电路。根据叠加原理可得
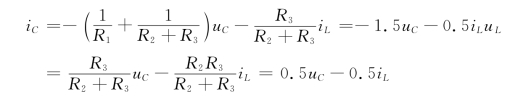
以q和ψ为状态变量，将uC=q3，iL=ψ3，
，
分别代入上两式，整理可得状态方程为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
