描述非线性动态电路的方程是非线性微分方程。电路理论中，把用一阶非线性微分方程描述的电路称为一阶非线性电路，典型的一阶非线性电路是只含有一个线性或非线性储能元件的非线性电路。同样，用二阶非线性微分方程描述的电路称为二阶非线性电路，典型的二阶非线性电路是只含有一个电感和一个电容的非线性电路。

建立非线性动态电路的输入—输出方程的基本依据仍然是两类约束。与线性动态电路一样，要完整地描述一个非线性动态电路，除了需要电路方程，还需要足够的初始条件，利用初始条件，才能解出待求的电路变量。

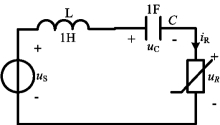
图11-27　例11-12图

例11-12　一含有非线性电阻的动态电路如图11-27所示，设电路中的电感和电容为线性的，非线性电阻的伏安关系为，试列写出该电路以iR为输出的输入—输出方程。

解　根据KVL和电感的VAR有

(www.daowen.com)

将非线性电阻的伏安关系代入上式得

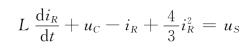
将上式两端对时间t求导，并利用电容的伏安关系，整理得该电路的输入—输出方程为

可见，非线性动态电路的输入—输出方程为非线性的微分方程。一般来说非线性的微分方程的解析形式是难以求得的，通常是利用计算机应用数值法来求得数值解。

当电路中所有元件均为时不变元件时，所列的微分方程不会显含时间变量t，这种由直流电源和时不变元件组成的电路称为自治电路，对应的方程则称为自治方程，否则称为非自治电路和非自治方程。显然，在例11-12中，若电压源为直流电源，即uS=US，电路为自治电路，所得到的方程也为自治方程。