小信号分析法（Small-signal Analysis）是电子工程上分析非线性电路的一个重要的常用方法，特别是电子电路中有关放大器的分析、设计就是以小信号分析为基础的。小信号是一个相对的概念，它通常是指电路中某一时变电量相对于直流电量而言，其幅值很小。例如在非线性电路中，有作为偏置电压的直流电源US作用，同时还有随时间变量的输入电压uS（t）作用，假设在任何时刻有，则把uS（t）称为小信号电压。

图11-24（a）所示电路中，直流电压源US为偏置电压，电阻R0为线性电阻，非线性电阻为压控型的，其伏安特性为i=g（u），曲线如图11-24（b）中曲线①所示。小信号时变电压为uS（t），且总成立。下面利用小信号法分析法求解非线性电阻的电压u（t）和电流i（t）。

图11-24　非线性电路小信号分析

（a）电路原理图；（b）非线性电阻的特性曲线；（c）小信号等效电路

对图11-24（a）所示电路应用KVL有

当uS（t）=0时，即电路中只有直流电压源作用时，负载线如图11-24（b）中直线②所示，它与非线性电阻伏安特性曲线的交点Q（UQ，IQ）即电路的静态工作点。在条件下，电路的解u（t）和i（t）必在工作点Q（UQ，IQ）附近，所以可以近似地把u（t）、i（t）写为

式中，u1（t）和i1（t）是由于信号uS（t）在工作点Q（UQ，IQ）附近引起的偏差。在任何时刻t，u1（t）和i1（t）相对于UQ，IQ都是很小的量。

考虑到给定非线性电阻的特性i=g（u），根据式（11-22）和式（11-23），可得

由于u1（t）很小，可以将式（11-24）在Q点附近用泰勒级数展开，并略去一次项以上的高效项，则有

由于IQ=g（UQ），所以式（11-25）可写成

又因为为非线性电阻在工作点Q（UQ，IQ）处的动态电导，所以有

由于在工作点Q（UQ，IQ）处是一个常量，所以由小信号电压uS（t）产生的电压u1（t）和电流i1（t）之间的关系是线性的。这样，式（11-21）可改写为

因为US=R0IQ+UQ，所以有

又因为在工作点Q（UQ，IQ）处，有u1（t）=Rdi1（t），代入式（11-28）得

式（11-30）是一个线性代数方程，由此可以作出给定非线性电阻在静态工作点Q（UQ，IQ）处的小信号等效电路，如图11-24（c）所示。于是求得非线性电阻的电压u（t）和电流i（t）分别为

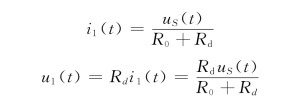
例11-10　在图11-25（a）中的非线性电阻电路中，非线性电阻的伏安特性为u=i+i2，uS=0.5sinωtV，试求回路中的电流i。

图11-25　例11-10图

解　由于激励包含有10V直流信号和小信号uS，所以可采用小信号分析方法求解。

令uS=0，则静态工作电流IQ满足

(www.daowen.com)

解得

IQ=2A 或 IQ=-5A

由图11-25（a）可知，I＞0，因此取IQ=2A。

静态工作占处的动态电阻为

作小信号等效电路如图11-25（b）所示，则

故得总电流为

例11-11　在图11-26（a），已知非线性电阻的伏安特性为

US=4V，uS（t）=15cosωtV。求电路的静态工作点Q以及Q点处uS（t）产生的电压Δu和电流Δi。

解　（1）求静态工作点。US=4V单独作用时，端口ab的戴维南等效电路如图11-26（b）所示。故可列出方程组为

u=2-50i

图11-26　例11-11图

联立求解得

u=1 和 u=-2V

因为u=-2V不在u≥0范围内，故该值应舍去，利用u=1进而又得。故工作点为

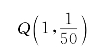
（2）求动态电导。

故可作出小信号等效电路，如图11-26（c）所示。

（3）根据小信号等效电路求解Q点处uS（t）产生的电压Δu和电流Δi。

Δu=2.5cosωtmV

Δi=0.1cosωtmA

综上所述，小信号分析法是一种局部线性化分析方法，其原理是利用工作点处特性曲线的切线近似代替该点附近的曲线，近似的程度取决于曲线与切线的接近程度。小信号分析法基本步骤为：

（1）求解非线性电路的静态工作点；

（2）求解非线性电路在静态工作点处的动态电导或动态电阻，将电路中的非线性电阻用动态电阻或电导替代，并将电路中的偏置电源置零，作出给定的非线性电阻在静态工作点处的小信号等效电路；

（3）根据小信号等效电路，计算仅由电路中的小信号作用引起的响应，即小信号解；

（4）计算电路的近似解。即静态工作点加上小信号解即为电路的近似解。