绝大多数非线性器件的特性曲线很难找到理想而精确的解析形式，而为了解析或数值地研究包含这种器件的电路，需要给出这种器件的数学表达式。因此，工程和理论上常用近似表示法逼近。分段线性化法（Piecewise Linear Approximation Method）是将非线性特性曲线用一系列折线段进行近似逼近，是目前分析非线性电路的一种最一般和非常重要的解析法，又称为折线近似法。其基本思想是，在一定允许工程误差要求下，将非线性元件复杂的伏安特性曲线用若干直线段构成的折线近似替代，即所谓分段线性化。由于各直线段所对应的线性区段分别对应于一个线性电路，所以可采用线性电路的分析计算方法，从而将非线性电路的求解转化为若干个结构和元件相同而参数各异的线性电路的分析计算。

图11-21（a）所示的二极管特性曲线，根据不同的分析精度要求，可分别采用图11-21（b）、图11-21（c）和图11-21（d）所示的分段线性化特性曲线来表示。在理想的情况下，在电压正向时，二极管完全导通，它相当于短路，在电压反向时，二极管截止，电流为零，它相当于开路，所以理想情况下二极管特性曲线如图11-21（b）所示；若不考虑二极管正偏时的导通阈值电压和反向饱和电流及击穿，则二极管特性曲线可用如图11-21（c）所示折线近似表示；若不考虑二极管的反向饱和电流和击穿而考虑它正偏导通的阈值电压，则二极管特性曲线可用如图11-21（d）所示折线近似表示。因此，一个元件的非线性特性曲线用多少折线段表示，是由分析精度要求决定的。自然，划分的段数越多，分段线性化特性越接近实际情况，但分析的工作量却随之迅速增加。在实际中可根据精度的要求采取折中的办法。

图11-21　二极管特性曲线分段化示例

（a）特性曲线；（b）（c）（d）分段线性化特性曲线

对于含有多个非线性电阻的电路，可以将其中每一个非线性电阻元件的伏安曲线用若干直线段近似表示，而对于每一直线段总可以得出其对应的戴维南等效电路或诺顿等效电路，因而可以在该直线段范围内，用所得到的戴维南等效电路或诺顿等效电路替代对应的非线性电阻元件，从而将其转换成线性电路来求解。由于每一非线性电阻的特性曲线都是由若干条直线段组成的，所以通常需要将所有直线段组合所对应的电路进行计算才能确定电路的解。

由于非线性电阻元件的工作状态不能超过该替代线性段的范围，而在求解电路过程中，并没有考虑每一个非线性电阻元件的确切工作范围，因此，需要在得出计算结果后检验每一线性电路计算结果的合理性。由于非线性电阻的每一直线段都位于一个电压和电流的取值区间，所以当用一条直线段对应的戴维南或诺顿等效电路来替代该非线性电阻时，即给定了这个电阻的电压和电流的取值范围，因此，若由直线段对应的等效电路计算得出的电压值和电流值都落在所给定的电压和电流的取值范围内，该计算结果就是正确的，即是电路的真实解；若计算出的电压值和电流值中只要有一个不在所给定的电压和电流的取值范围内，则该计算结果就是不合理的，即不是电路的真实解，应予剔除。一旦求得非线性电阻上的电压或电流值，则可以利用含戴维南或诺顿等效电路的线性求出原非线性电路中任意支路的电压和电流。

例11-8　图11-22（a）中的虚线为隧道二极管的伏安特性曲线，用分段线性化法讨论其伏安特性。

解　图11-22（a）中，隧道二极管的伏安特性曲线可用图示的三段直线粗略表示。假设这三段直线的斜率分别为：

G=Ga，当u≤U1　

G=Gb，当U1＜u≤U2

G=Gc，当u＞U2　

其中U1，U2确定了这三个区域，而U1和U2为转折点的电压值。该伏安特性可分解为三个伏安特性，即图11-22（b）中直线，折线和，并设图11-22（b）中有关直线段的斜率分别为G1，G2和G3，根据非线性电阻并联图解法原则，就可以确定G1，G2和G3。

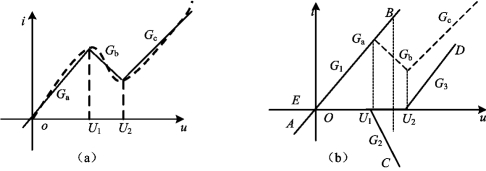
图11-22　例11-8图

当u≤U1时

G1u=Gau 或 G1=Ga

当U1＜u≤U2时

G1u+G2u=Gbu 或 G1+G2=Gb

当u＞U2时

G1u+G2u+G3u=Gcu 或 G1+G2+G3=Gc

因此，可得

G1=Ga， G2=Gb-Ga， G3=Gc-Gb(www.daowen.com)

故隧道二极管的伏安特性曲线可以看成G1，G2和G3三个电导并联后的等效电导的伏安特性。

例11-9　在图11-23（a）中的非线性电阻R1，R2的伏安特性曲线分别用折线逼近，如图11-23（b）和（c）所示。试求I1和U2。

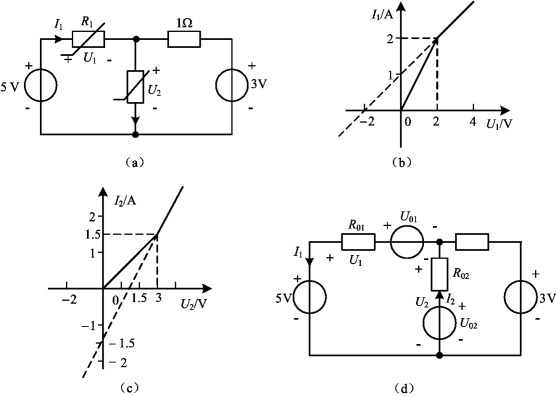
图11-23　例11-9图

（a）原电路；（b）R1的伏安特性曲线；（c）R2的伏安特性曲线；（d）作戴维南等效后的电路

解　（1）根据R1，R2的伏安特性曲线讨论其对应戴维南电路中的各元件参数。

由图11-23（b）可知，对R1而言，当0＜I1≤2A时，R1为一线性电阻有

R01=1Ω， U01=0

当I1≥2A时，R1为一戴维南电路有

R01=2Ω， U01=-2V

由图11-23（c）可知，对R2而言，当0＜U2≤3V时，R2为一线性电阻有

R02=2Ω， U02=0

当U2≥3V时，R2为一戴维南电路有

R02=1Ω， U01=1.5V

于是可得到图11-23（d）所示的等效电路。

（2）对图11-23（d）所示的电路应用KVL和KCL，可得

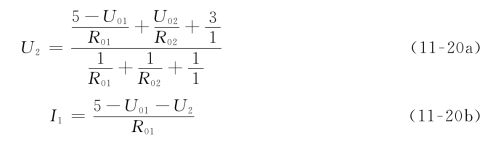
（3）分别对R1，R2伏安特性各直线段组合求解。

①将R01=1Ω，U01=0和R02=2Ω，U02=0组合代入式（11-20a）和式（11-20b），求得U2=3.2V，I1=1.8A，由于U2=3.2V超出了式R02=2Ω，U02=0成立的范围（0＜U2≤3V），所以不是解；

②将R01=1Ω，U01=0和R02=1Ω，U02=1.5V组合代入式（11-20a）和式（11-20b），求得U2≈3.17V，I1=1.83A，该结果在R01=1Ω，U01=0和R02=1Ω，U02=1.5V成立的范围之内，故是所求解；

③将R01=2Ω，U01=-2V和R02=2Ω，U02=0组合代入式（11-20a）和式（11-20b），求得U2=3.25V，I1=1.875A，由于U2=3.25V超出了式R02=2Ω，U02=0成立的范围（0＜U2≤3V），所以不是解；

④将R01=2Ω，U01=-2V和R02=1Ω，U02=1.5V组合代入式（11-20a）和式（11-20b），求得U2=3.2V，I1=1.9A，由于I1不在R02=1Ω，U02=1.5V成立的范围（I1≥2A）之内，所以不是解；

综上所述，可知所求得的解为U2≈3.17V，I1=1.83A。