线性电阻电路中介绍的各种建立电路方程的方法可以推广到非线性电阻电路。对于简单的非线性电阻电路，可以先采用2b法即直接列写独立的KVL、KCL以及元件的VAR，再通过将VAR方程代入到KVL、KCL方程中消去尽可能多的电流、电压变量，从而得到方程数目最少的电路方程，这种方法称为代入消元法，可以用于既有压控型又有流控型非线性电阻的非线性电路；若电路中的非线性电阻均为压控型或单调电阻，则宜节点法列写非线性电阻电路方程；若电路中的非线性电阻均为流控型或单调电阻，则宜选用回路法或网孔法列写非线性电阻电路方程；当电路中既有压控型电阻又有流控型电阻时，直接建立节点电压方程的过程就会比较复杂；当电路中既有流控型电阻又有压控型电阻时，直接建立回路方程的过程就会比较复杂。下面通过实例来说明上述概念。

例11-2　在如图11-12所示的非线性电路中，已知IS=2A，R1=2Ω，R2=6Ω，US=7V，非线性电阻是流控型的，有，试求uR1之值。

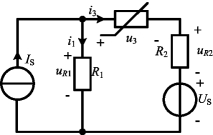
图11-12　例11-2图

解　对图11-12中节点，应用KCL有

i1+i3=IS

对图11-12中右回路，应用KVL有

u3+uR2-uR1+US=0

又元件的伏安关系为

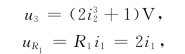
联立以上几式，可得

解得

由此可见，非线性电路的解不是唯一的。

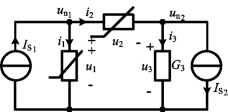
例11-3　电路如图11-13所示，两个非线性电阻元件的伏安关系分别为：.，，试列出该电路的节点电压方程。

解　根据KCL得

(www.daowen.com)

图11-13　例11-3图

根据KVL得

又电阻元件的伏安关系为

将上述方程组中的非节点电压变量消去，可得下列节点电压方程

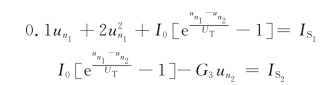
例11-4　电路如图11-14所示，非线性电阻的特性方程分别为，u3=sini3，试列出该电路的网孔电流方程。

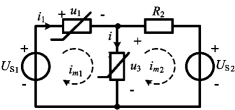
图11-14　例11-4图

解　设网孔电流参考方向如图11-14中虚线所示，则有

对各网孔列写KVL方程，并考虑各元件的VAR，可得网孔电流方程

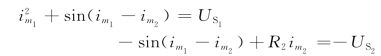
由以上实例不能推出，非线性电阻电路的方程可写成下列一般形式

式（11-15）中，x1，x2，…，xn是n个独立电压或（和）电流变量。如果所讨论的电路中含有时变电源时，式（11-15）中还得加上时间参变量t。显然，上述非线性代数方程一般难以求得解析解，只能依靠计算机应用数值法求解。