线性电感也是一个两端储能元件，其特征是用磁通链ψ与电流i之间的函数或韦安特性表示的。若电感的韦安特性曲线不是一条通过ψ～i平面坐标原点的直线，则为非线性电感，非线性电感的电路符号如图11-8所示。

根据非线性电感的韦安特性曲线，非线性电感也可分为四种类型：流控电感、链控电感、单调电感和多值电感。

若非线性电感的电流i与磁通链ψ的关系表示为

i=h（ψ）

即电流是磁链的单值函数，则称为磁通链控制的电感。约瑟夫逊结是一种典型的链控电感，其韦安特性方程为

i=I0sin（Kψ）

式中，I0、K均为常数。

若非电流与磁链的关系表示为

ψ=f（i）

即磁链是电流的单值函数，则称为电流控制的电感。

若电流和磁链是单调函数，即既可记作i=h（ψ），又可记作ψ=f（i），则称为单调型。一般铁芯线圈在忽略损耗和磁滞影响时的电路模型就是单调型非线性电感。其韦安特性曲线如图11-9所示，可见，当电流较大时，磁通增大极为缓慢，即磁通已达到饱和。显然，单调电感既是链控电感也是流控电感。

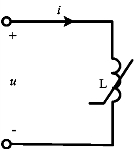
图11-8　非线性电感电路符号

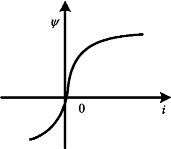
图11-9　一般铁芯线圈的特性曲线

多值电感既不能把磁链表示成电流的单值函数，也不能把电流表示成磁链的单值函数，亦即不是流控的也不是链控的。若磁滞影响不可忽略，则铁芯线圈就是一个典型的多值电感，其在正弦电流激励下的韦安特性曲线如图11-10所示，该闭合曲线称为磁滞回线。

同样为了计算方便，对于非线性电感也引入静态电感LS和动态电感Ld两个概念。

电感韦安曲线上任一工作点P的静态电感LS的定义为该点的磁链坐标值与电流坐标值之比，即

电感韦安曲线上任一工作点P的动态电感Ld的定义为该点切线的斜率，即

如图11-11所示的非线性电感韦安特性曲线上P点的静态电感LS正比于tanα，动态电感Ld正比于tanβ。静态电感LS和动态电感Ld一般都是磁通链ψ和电流i的函数。(www.daowen.com)

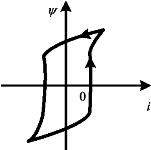
图11-10　铁芯线圈的ψ～i特性曲线

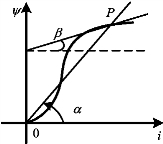
图11-11　非线性电感的静态和动态电感示例

当磁链是电流的单值函数时，非线性电感的电压和电流之间的关系为

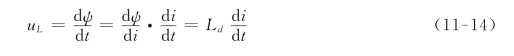
例11-1　设有一个非线性电阻元件，其伏安特性为u=f（i）=3i-4i3。

（1）试分别求出i1=10A，i2=1A，i3=0.1A，i4=0.01A，i5=0.001A时对应的电压u1，u2，u3，u4，u5的值；

（2）试求i=sinωA时对应的电压u的值；

（3）设u12=f（i1+i2），试问u12是否等于u1+u2？

解　（1）i1=10A时，u1=3×10-4×103=[30-4×103]V

i2=1A时，u1=3×1-4×13=-1V

i3=0.1A时，u2=3×0.1-4×（0.1）3=（0.3-4×10-3）V

i4=0.01A时，u4=3×0.01+（0.01）3=（0.03-4×10-6）V

i5=0.001A，u5=3×0.001-4×（0.001）3=（0.003-4×10-9）V

计算说明当电流i不同时，引起的误差不同，当电流较小时，引起的误差不大。因此，这一非线性电阻元件在较小电流情况下，可作线性电阻处理。

（2）当i=sinωA时，u=3×sinωt-4sin3ωt=sin3ωtV

电压u中含有3倍于电流频率的分量，所以此流控非线性电阻实际上就是一种变频器，因此利用非线性电阻可以产生频率不同于输入频率的输出，这种作用称为“倍频”。实际上，电阻元件的作用已经远远超出了“将电能转化为热能”的范围，在现代电子技术中，非线性电阻和线性时变电阻被广泛地应用于整流、变频、调制、限幅等信号处理的诸多方面。

（3）设u12=f（i1+i2），则

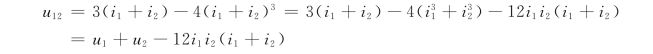
可见，一般i1+i2≠0，因此有u12≠u1+u2。这就是说叠加定理不适用于非线性电路。