回转器是一种线性非互易的多端元件,它的电路符号如图10-32所示。理想回转器可视为一个二端口,它的端口电压、电流关系可表示为:
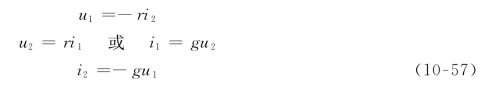
式(10-57)的另一种形式为
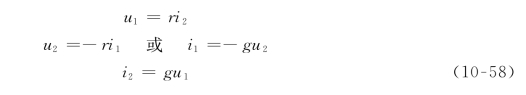
上两式中,r称为回转电阻,g称为回转电导,两者统称为回转常数,它们分别具有电阻和电导的量纲。为了区别这两种形式,习惯在图10-32所示电路符号图上方加一个箭头表示回转方向:当箭头自左指向右时,它对应于式(10-57),而当箭头自右指向左时,它对应于式(10-58)。式(10-57)也称为回转器的特性方程。式(10-58)是回转器特性方程的另一种形式。
式(10-57)的矩阵形式为
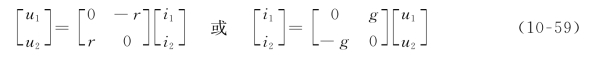
可见,回转器的Z参数矩阵和Y参数矩阵分别为

若在端口2-2′接上一个电容元件,如图10-33所示。将电容元件的伏安关系特性方程![]() 代入回转器的端口方程式(10-57)可得
代入回转器的端口方程式(10-57)可得
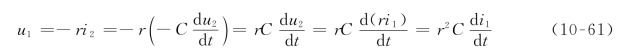
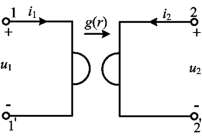
图10-32 回转器电路模型
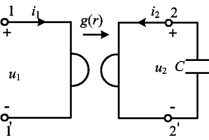
图10-33 用回转器实现电感的电路
将式(10-61)与电感元件的伏安关系式比较可得
![]()
由此可见,图10-33所示电路中端口1-1′对外等效于一个电感值为L=r2C的电感元件。
同理,若在端口2-2′接上一个电感元件,将电感元件的伏安关系![]() 代入回转器的端口方程式(10-57)可得
代入回转器的端口方程式(10-57)可得
![]()
将式(10-63)与电容元件的伏安关系式比较可得
![]()
可见,回转器可将其一个端口的电流(或电压)“回转”为另一个端口的电压(或电流),因此,回转器可以把一个电容(或电感)回转为一个电感(或电容)。
根据回转器特性方程以及图10-32中的参考方向,可得输入给回转器的总功率为:
![]()
这表明回转器在任何时刻的功率为零。即它既不消耗功率也不产生功率,故回转器为一无源线性元件。
由回转器特性方程的矩阵形式可知,其Z参数矩阵的Z12≠Z21,所以回转器是一个非互易的二端口元件,互易定理不适用于回转器。
例10-18 试说明图10-34为实现一个回转的电路,并求其特性方程。
解 设图中对应各节点电压分别为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,应用节点分析法分别对节点①、②、④、⑥列写节点方程可得
,应用节点分析法分别对节点①、②、④、⑥列写节点方程可得
节点①
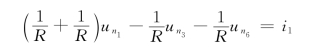
节点②
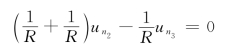
节点④
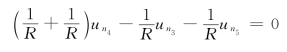
节点⑥
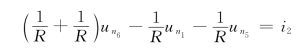
根据理想运算放大器的“虚断”和“虚短”特性有
![]()
将上式代入节点方程中得(https://www.daowen.com)
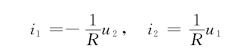
此即为二端口电路两个端口的电压、电流特性方程,即图10-32所示电路的回转器特性方程。因此,可得到其Y参数为
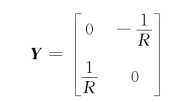
因此,图10-34是一个用运算放大器实现的回转器电路。
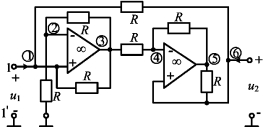
图10-34 例10-18图
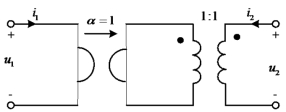
图10-35 例10-19图
例10-19 试求图10-35所示二端口电路的传输矩阵。
解 图10-35所示二端口电路可分解为由回转器和理想变压器组成的两个二端电路的级联电路。
回转器的端口方程为
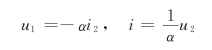
所以回转器的传输矩阵为

理想变压器的端口方程为
u1=u2
i1=-i2
所以理想变压器的传输矩阵为

所以,复合二端口电路传输矩阵为
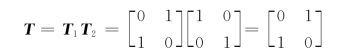
例10-20 试求图10-36所示二端口电路的短路导纳矩阵。
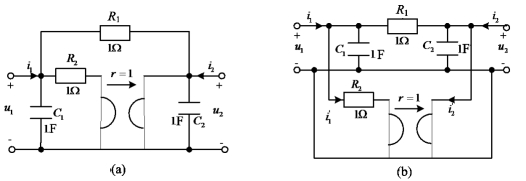
图10-36 例10-20图
解 将图10-36(a)所示二端口电路拆分为两个二端口电路的并联,如图10-36(b)所示。这是两个三端电路的并联,若将两个三端电路的公共端连接在一起,则该并联连接为有效连接。因此,图10-36(b)中上面一个二端口电路的Y参数矩阵为
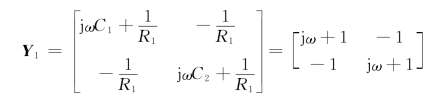
由图10-36(b)中下面一个二端口电路可得
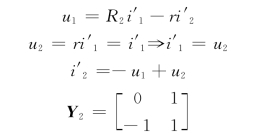
因此,复合二端口电路的导纳矩阵为
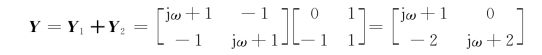
例10-21 试证明两个回转器级联后(如图10-37(a)),可等效为一个理想变压器(如图10-37(b)),并求出变比n与两个回转器的回转电导g1和g2的关系。
证明:由回转器的端口特性方程可得图10-37(a)复合二端口的T参数矩阵为
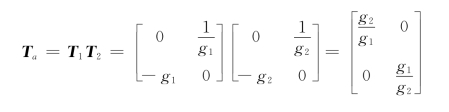
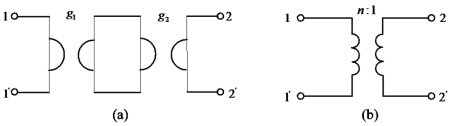
图10-37 例10-21图
图10-37(b)所示变压器的T参数矩阵为
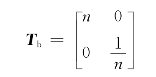
比较Ta和Tb可得,两个级联的回转器可等效为一个理想变压器,其等效变比为
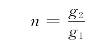
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





