在实际应用中,二端口电路的输入端口接信号源,输出端口接负载,其端口电压、电流由信号源、二端口电路和负载共同决定。这时,常常采用网络函数概念研究二端口电路的实际工作特性。由第七章讨论可知,响应相量与激励相量之比称为传递函数,或称网络函数。激励和响应在同一端口的网络函数称为策动点函数,否则称为转移函数。由于激励、响应可以是电压或电流相量,因此网络函数有输入阻抗、输入导纳、输出阻抗、输出导纳、转移阻抗、转移导纳、电压比和电流比等多种形式。下面讨论二端口电路的网络函数。
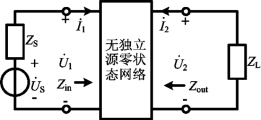
图10-19 具双端接二端口网络的等效电路
图10-19所示为具有双端接二端口网络的等效电路,所谓双端接指的是两个端口均接上一个单口网络,通常输入端口所接的网络含独立电源,可等效为一个戴维南电路;输出端口所接的是无源单口网络,可等效为一个无源负载支路。
前面对二端口的讨论都是按正弦稳态情况考虑的,故用相量分析法,若用运算法分析二端口,则电路中各参数都是复变量s的函数。由图10-19所示电路可以写出Z参数方程及二端口外接端口的电压、电流关系为
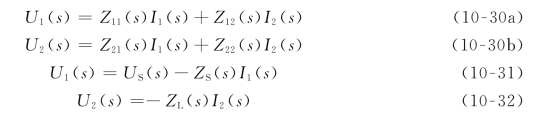
由式(10-30b)和式(10-32)得![]() 代入式(10-30a)中得
代入式(10-30a)中得
![]()
所以,用Z参数表示的输入阻抗即输入端口的策动点阻抗为

由式(10-33)可见,输入端口的策动点阻抗是网络复频域参数的函数,且和负载阻抗ZL(s)有关。因此,对于同一个二端口,其输出端口接不同的负载,可得到不同的输入阻抗Zin(s);而同一负载ZL(s)接于不同的二端口,输入阻抗Zin(s)也是不同的。这表明,二端口电路具有变换阻抗的作用,即为一阻抗变换器或转换器。
由式(10-30a)和式(10-31)得![]() 代入(10-30b)中得
代入(10-30b)中得
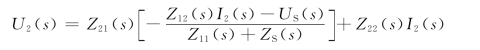
由输出阻抗定义,令US(s)=0,则可得用Z参数表示的输出阻抗即输出端口的策动点阻抗为
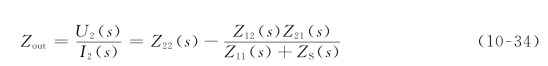
由式(10-34)可见,输出端口的策动点阻抗也是网络复频域参数的函数,且和接入端口的阻抗ZS(s)有关。由于此时US(s)=0,ZS(s)相当于输入口所接负载,因此,也说明二端口电路具有变换阻抗的作用,即为一阻抗变换器或转换器。
由式(10-30b)和式(10-32)得![]() 代入式(10-30a)中得
代入式(10-30a)中得
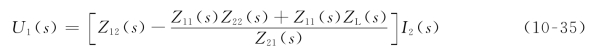
由转移电压比定义和式(10-32)、式(10-35)可得,用Z参数表示的端口转移电压比为
![]()
用Z参数表示的端口转移电流比为
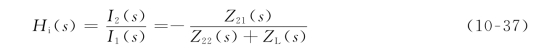
由式(10-36)可求得电压增益为
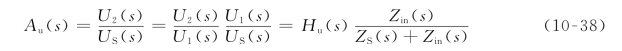
电流增益为
![]()
类似的方法可以求得其他参数表示的策动点阻抗、转移电压比、转移电流比、电压增益和电流增益等相关参数。
例10-10 图10-20所示二端口N处于正弦稳态,若在端口2-2′处连接负载![]() 求端口1-1′处的输入阻抗;若在端口1-1′处连接负载
求端口1-1′处的输入阻抗;若在端口1-1′处连接负载![]() 求端口2-2′处的输出阻抗。
求端口2-2′处的输出阻抗。
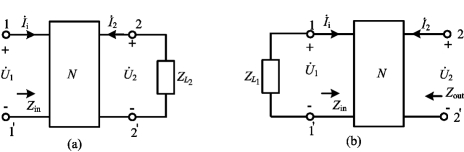
图10-20 例10-10图
解 由图10-20(a)可得T参数方程为

端口1-1′处的输入阻抗
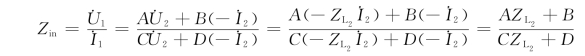
由T参数方程可得(https://www.daowen.com)

若在端口1-1′处连接负载![]() ,如图10-20(b)所示,考虑到
,如图10-20(b)所示,考虑到![]() ,端口2-2′处的输出阻抗
,端口2-2′处的输出阻抗
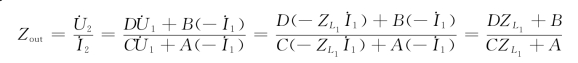
对于对称二端口电路,因为A=D,则有
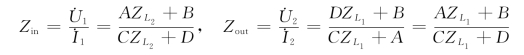
由此可见,若![]() ,则有Zin=Zout。若进一步使
,则有Zin=Zout。若进一步使![]() ,正好使Zin=Zout=ZC,则有
,正好使Zin=Zout=ZC,则有
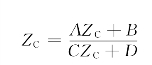
即有![]() ,由于A=D,所以有
,由于A=D,所以有
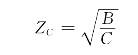
由于上式仅仅决定于二端口电路参数,因此称它为二端口电路的特性阻抗。
以上所述表明,对于对称二端口电路,若在其端口2-2′(或1-1′)处接以特性阻抗ZC,则从端口1-1′(或2-2′)处看进去的输入阻抗恰好是这个特性阻抗ZC,因此,ZC又称为重复阻抗。
例10-11 图10-21所示线性二端口网络N,当RL→∞时,U2=7.5V,当RL=0时,I1=3A,I2=-1A。(1)求二端口网络的Y参数;(2)求二端口网络的三角形等效电路系统;(3)求当RL=何值时,RL可获得最大功率,并求最大功率Pmax。
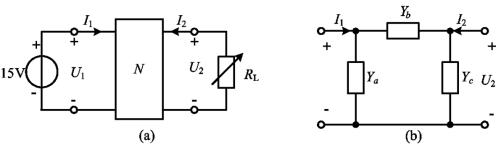
图10-21 例10-11图
解 (1)Y参数方程为
I1=Y11U1+Y12U2
I2=Y21U1+Y22U2
线性电阻二端口网络N一定是互易的,所以有:Y12=Y21。
当RL→∞时,U2=7.5V,I2=0有
15Y21+7.5Y22=0
当RL=0时,I1=3A,I2=-1A,代入Y参数方程第一式中有
I1=3A=15Y11+0×Y12, I2=-1A=15Y21+0×Y22
所以,有![]() ,
,![]() ,
,![]() ,所以Y参数矩阵为
,所以Y参数矩阵为
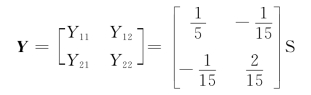
(2)设二端口网络的三角形等效电路如图10-21(b)所示,对应的方程为
I1=(Ya+Yb)U1-YbU2
I2=-YU1+(Yb+Yc)U2
与(1)中Y参数比较,可得![]() ,
,![]() 。
。
(3)先求戴维南等效电路。当U1=0时,输出端口的电阻为
![]()
当I2=0时,输出端口的开路电压为
![]()
所以,当![]() 时,可获得最大功率,最大功率为
时,可获得最大功率,最大功率为
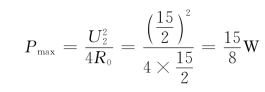
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






