若选择端口1-1′的电流![]() 和端口2-2′的电压
和端口2-2′的电压![]() 作独立变量,即以它们构成二端口电路的激励源,而以端口1-1′的电压
作独立变量,即以它们构成二端口电路的激励源,而以端口1-1′的电压![]() 和端口2-2′的电流
和端口2-2′的电流![]() 作为响应,如图10-11所示。则根据叠加定理可得端口特性方程为
作为响应,如图10-11所示。则根据叠加定理可得端口特性方程为

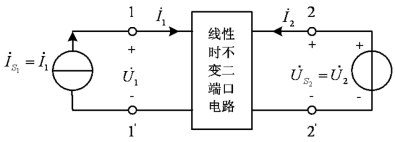
图10-11 由电流源和电压源驱动的线性二端口电路
其矩阵表达式为
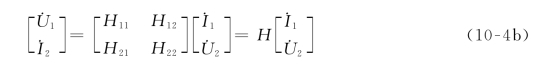
式中,Hjk(j=12;k=12)称为二端口特性方程的参数,称为H参数(H Parameters),因为H参数的量纲分别是阻抗、导纳或无量纲,所以又称为混合参数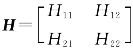 称为H参数矩阵或称为混合参数矩阵。H参数的值可以分别令
称为H参数矩阵或称为混合参数矩阵。H参数的值可以分别令![]() (输出端口短路)与
(输出端口短路)与![]() (输入端口开路)来求得:
(输入端口开路)来求得:
![]() 称为端口2-2′短路时,端口1-1′处的策动点阻抗,具有阻抗量纲;
称为端口2-2′短路时,端口1-1′处的策动点阻抗,具有阻抗量纲;
![]() 称为端口2-2′短路时,正向转移电流比,无量纲;
称为端口2-2′短路时,正向转移电流比,无量纲;
![]() 称为端口1-1′开路时反向转移电压比,无量纲;
称为端口1-1′开路时反向转移电压比,无量纲;
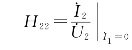 称为端口1-1′开路时,端口2-2′策动点导纳,具有导纳量纲。
称为端口1-1′开路时,端口2-2′策动点导纳,具有导纳量纲。
由于H参数能直接从晶体静态特性曲线获得,而且在低频时都是实数,容易用实验的方法直接测量出来,因此它在低频小信号晶体管放大器电路的分析中得到了广泛应用。
计算H参数的过程与求Z参数或Y参数的过程相类似。根据所要计算的参数,在适当的端口加上电压源或电流源,再短路或开路另一个端口,按定义就能得到H值。
若选取![]() 和
和![]() 为独立变量分别作为端口1-1′和端口2-2′的电压源和电流源激励,而以
为独立变量分别作为端口1-1′和端口2-2′的电压源和电流源激励,而以![]() 和
和![]() 为响应,则端口方程为
为响应,则端口方程为
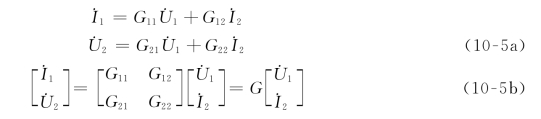
便得到另一种混合参数即G参数。在式(10-5)中分别令![]() 和
和![]() 便可得到G参数物理意义的表示式。G参数的求解方法可与H参数的作类比得到。但G参数实际较少使用,有时用于分析电子工程反馈放大器等。
便可得到G参数物理意义的表示式。G参数的求解方法可与H参数的作类比得到。但G参数实际较少使用,有时用于分析电子工程反馈放大器等。
例10-6 求图10-12所示二端口电路的H参数矩阵。
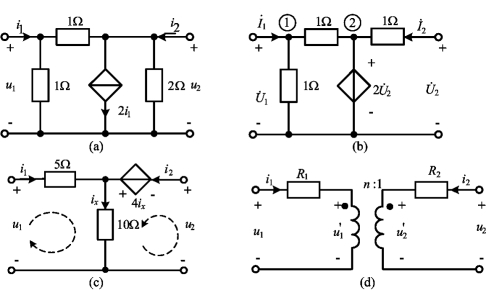
图10-12 例10-6图
解 对图(a),用H参数物理意义求解。令u2=0,则有
u1=1×(2i1-i2), u1=1×[i1-(2i1-i2)]
可求得![]() ,
, ![]()
因此
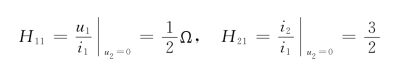
令i1=0,则有2i1=0,即受控源开路,且左侧两个1Ω电阻串联后再与右侧2Ω并联分流有
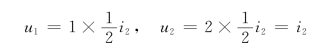
因此(https://www.daowen.com)
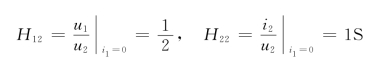
所以,图10-12(a)所示电路的H参数矩阵为

对图(b)采用节点分析法来求二端口电路方程,列写节点①、②方程为
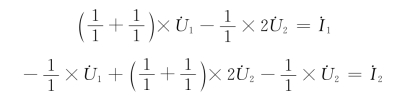
整理得
![]()
所以,图10-12(b)所示电路的H参数矩阵为
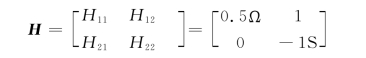
对图(c)列写回路电流方程如下
(5+10)i1+10i2=u1
10i1+10i2=u2+4ix
又
ix=i1+i2
整理得
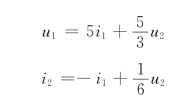
所以,图10-12(c)所示电路的H参数矩阵为
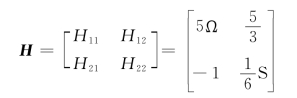
对图(d)根据KVL和理想变压器方程得
u1=R1i1+nu′2
i2=-ni1
u′2=u2-R2i2
整理得
u1=(R1+n2R2)i1+nu2
i2=-ni1
所以,图10-12(d)所示电路的H参数矩阵为
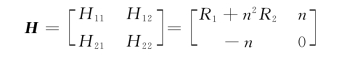
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






