若选取二端口电路的端口电流![]() 和
和![]() 作为独立变量,以端口电压
作为独立变量,以端口电压![]() 和
和![]() 为因变量,即一个二端口电路同时由两个电流源
为因变量,即一个二端口电路同时由两个电流源![]() 和
和![]() 驱动,以两端口电压
驱动,以两端口电压![]() 和
和![]() 为响应,如图10-4所示。由于所研究的是线性时不变无源二端口电路,所以当
为响应,如图10-4所示。由于所研究的是线性时不变无源二端口电路,所以当![]() 和
和![]() 分别单独作用时,响应
分别单独作用时,响应![]() 和
和![]() 的关系分别满足叠加定理,因此,可以得到如下的端口特性方程
的关系分别满足叠加定理,因此,可以得到如下的端口特性方程

其矩阵表达式为:
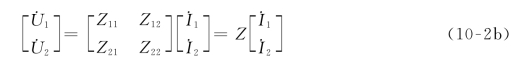
式(10-2)为描述二端口的特性方程,Zjk(j=1,2;k=1,2)称为描述二端口电压变量![]() 和
和![]() 与端口电流变量
与端口电流变量![]() 和
和![]() 之间关系的端口方程的参数,称为Z参数(Z-Parameters)
之间关系的端口方程的参数,称为Z参数(Z-Parameters)![]()
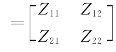 称为Z参数矩阵或称为阻抗参数矩阵。Z参数的值可以分别令
称为Z参数矩阵或称为阻抗参数矩阵。Z参数的值可以分别令
![]() (输入端口开路)与
(输入端口开路)与![]() (输出端口开路)来求得:
(输出端口开路)来求得:
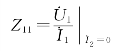 称为端口2-2′开路时,端口1-1′处的开路输入阻抗
称为端口2-2′开路时,端口1-1′处的开路输入阻抗
![]() 称为端口2-2′开路时,端口2-2′与端口1-1′间的开路转移阻抗
称为端口2-2′开路时,端口2-2′与端口1-1′间的开路转移阻抗
![]() 称为端口1-1′开路时,端口1-1′与端口2-2′间的开路转移阻抗
称为端口1-1′开路时,端口1-1′与端口2-2′间的开路转移阻抗
![]() 称为端口1-1′开路时,端口2-2′处的开路输出阻抗
称为端口1-1′开路时,端口2-2′处的开路输出阻抗
由于Z参数都是在开路情况下测量或直接计算求得的,故习惯上称为开路阻抗参数(Open-circuit Impedance Parameters),Z参数同时也是一种网络函数。Z参数在电路综合中有着广泛的应用,也用于分析电子工程中串-串连接反馈放大器等。
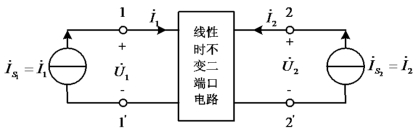
图10-4 由电流源驱动的线性二端口电路
由于Z11由端口1-1′的电压和电流决定,而Z22由端口2-2′的电压和电流决定,因此Z11和Z22也称为驱动点阻抗;Z12端口1-1′的端口电压和端口2-2′的电流决定,而Z21由端口2-2′的端口电压和端口1-1′的电流决定,因此Z12和Z21也称为转移阻抗。
若Z11=Z22,则该二端口称为对称二端口。当二端口是线性无源网络时,若转移阻抗相等(Z12=Z21)则该二端口为互易的二端口。对互易二端口,它们的激励点和响应互换时,其转移阻抗不变。任意一个二端口若全部由电阻、电容和电感所构成,则该二端口必然是互易的。
例10-1 求图10-5所示电路的Z参数。
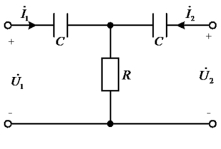
图10-5 例10-1图
根据Z参数物理意义,求得
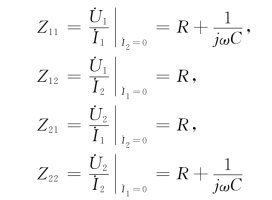
所以,Z参数矩阵为
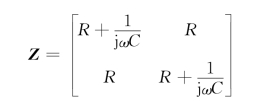
也可以利用网络互易对称来求解Z21和Z22:Z21=Z12,Z22=Z11。
例10-2 求图10-6所示电路的Z参数。(https://www.daowen.com)
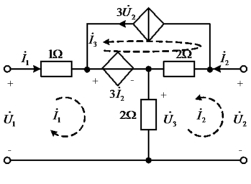
图10-6 例10-2图
解 选取如图10-6所示的3个网孔,则3个网孔电流分别为![]() 、
、![]() 和
和![]() ,根据网孔分析法,可得各网孔电流方程为
,根据网孔分析法,可得各网孔电流方程为
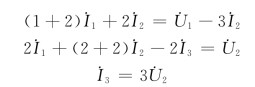
联立求解上述3个方程,可得
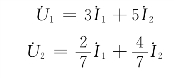
或
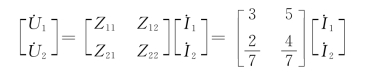
由此可得Z参数分别为
![]()
例10-3 图10-7所示电路,已知S打开时![]() ,
,![]() ;S闭合时
;S闭合时![]() ,
,![]() ,ZL=10+j5Ω。求Z参数。
,ZL=10+j5Ω。求Z参数。
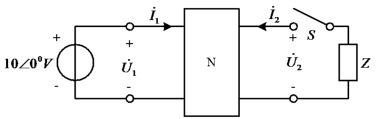
图10-7 例10-3图
解 对于二端口电路有
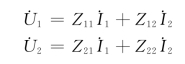
故当![]() 时有
时有
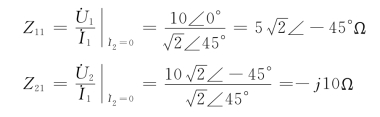
当S闭合时有
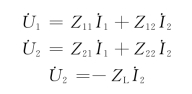
将![]() ,
,![]() ,ZL=10+j5Ω代入上述3个式中联立求得到
,ZL=10+j5Ω代入上述3个式中联立求得到
Z12=-j10Ω,Z22=-j15Ω
故得求Z参数为
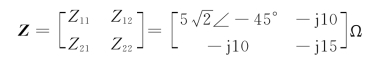
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






