实际发电机发出的电压波形并不是理想的正弦波，而是周期性的非正弦波。但因发电机结构的对称，电压波形总是对称于横轴，因而它只含奇次谐波。所以，在对称的三相电路中，电压和电流都可能含有高次谐波分量。在对称三相电路中，各相电压虽然是非正弦的，但其变化规律仍然相同，只是在时间上依次相差个周期。设A相电压为uA（t）=u（t），则B相和C相的电压分别为

由于发电机的每相电压为奇次谐波函数，所以将对称三相电压展开为傅里叶级数，有

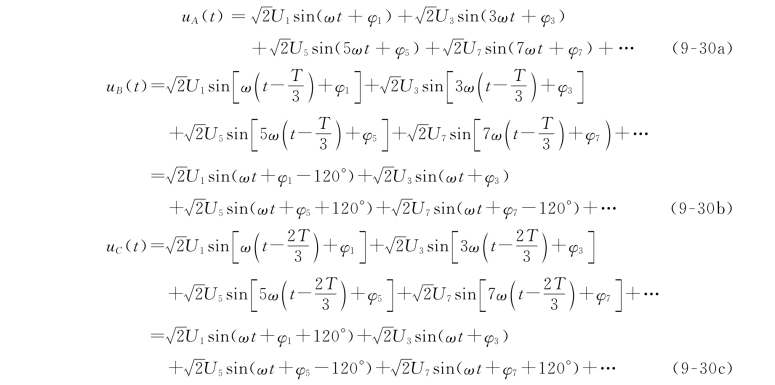
上述运算中用到了kωt=2kπ。

由上述各式可以看出，基波、7次谐波、13次谐波、19次谐波等分量分别都是对称的三相电压，组成相序为A-B-C三相电压，即正序（Positive Sequence）；5次谐波、11次谐波、17次谐波等分量也是对称的三相电压，组成相序为A-C-B三相电压，即逆序（Negative Sequence）；而3次谐波、9次谐波、15次谐波等分量 的电 压相 位相同，即 为 零 序（Zero Sequence）。可见，6k+1（k=0，1，2，…）次谐波构成一组正序对称组，6k+5（k=0，1，2，…）次谐波构成一组负序对称组，而6k+3（k=0，1，2，…）次谐波构成一组零序对称组。所以，对称的三相非正弦周期电压的谐波分量可以看成是由以上三类对称组组成的，即由正序对称组、负序对称组和零序对称组。

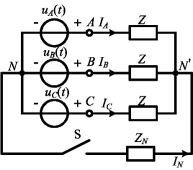
图9-14　Y-Y连接时的高次谐波

在上述对称的非正序周期电压源作用下的对称三相电路的分析计算，按上述三类对称组分别进行。对于正序和负序对称组，可直接引用对称三相电路的计算方法和结论，对于零序组电源对对称三相电路作用，与系统的连接方式有关。

（1）对称的Y形电源

当对称三相非正弦电源星形连接时，如图9-14所示。

由KVL可得

uAB（t）=uA（t）-uB（t）， uBC（t）=uB（t）-uC（t）， uCA（t）=uC（t）-uA（t）

由于电源相电压包含有全部谐波分量，利用三相电源表达式，可得电源相电压的有效值为

而线电压等于相应的两个相电压之差。对于零序谐波而言，由于三相电压的大小和相位相同，故虽然相电压中有零序谐波分量，但线电压中却无零序谐波分量。对于正序三相电压组和负序三相电压组相电压之间由于相差120°，其对应的线电压中各次谐波分量的有效值等于相电压中同次谐波有效值的倍。由上述分析可知，电源的线电压的有效值为

(www.daowen.com)

可见，线电压并不是相电压的倍，而是。

若三相负载也为Y形连接，如图9-14所示。如果电源与负载之间有中线，即图9-14所示电路中的开关S闭合时，正负序谐波的相电压在中线上不会产生电流。但电源相电压的零序谐波分量将传至各相负载，从而在负载中产生零序谐波分量电流，这些相电流都以中线为返回路径，因此，中线上的电流是各相电流零序谐波分量的3倍，即

零序谐波电流在负载上产生零序谐波电压，因负载相电压中的同次序谐波大小相等且相同，故负载线电压中不含零序谐波分量。因此，不论电源侧还是负载侧，线电压中均无零序谐波分量，线电压有效值都小于相电压有效值的倍。

如果电源与负载之间有无中线，即图9-14所示电路中的开关S断开时，由于加在负载上的线电压中无零序谐波，因此，在负载相电压中只有正序、负序谐波而没有零序谐波。故对正序、负序谐波分量电压而言，仍可分别用相量法按照对称三相电路归结为一相的计算方法来处理。负载线电压的有效值仍为相电压有效值的倍。由于电源相电压中无零序谐波，这就使得电源中性点和负载中性点之间的电压不为零，而等于零序谐波分量，即

而且线电流、相电流中无零序谐波分量。

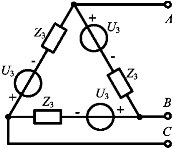
图9-15　△形连接时零序环流计算

（2）对称的三角形电源

当对称三相电路的电源成三角形连接时，如图9-15所示。电源回路中正、负序三相电压组的电压之和为零，而电源相电压中的零序谐波组，如3次谐波，沿电源回路之和将不等于零，而等于每个相电压中该谐波分量的3倍。回路中将有3k（k=1，3，5，…）次谐波的环行电流，其有效值为

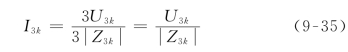
式中，为每相电源对3k（k=1，3，5，…）次谐波的内阻抗。

由于上述环流在内阻抗上的电压和相电压的零序谐波分量之和恰好为零，所以，三角形端线电压只含正、负序对称成分，即

为了避免电源中零序谐波环电流，工程中三相发电机一般不用三角形连接，而按Y形连接。