有源滤波器由电阻、电容和运算放大器等组成，它不需要电感，能提供增益放大，还可以和缓冲放大器结合使用，将滤波器与电源和负载阻抗的影响隔开，正好克服了无源滤波器增益小于1，不能增加网络的能量，可能需要笨重和较贵的电感元件等不足。但有源滤波器的可靠性和稳定性差，大多数有源滤波器其实际工作频率限制在100kHz以下，一般的有源滤波器的工作频率远低于100kHz。有源滤波器有低通滤波器、高通滤波器、带通滤波器和带阻滤波器等几种形式。

1.一阶低通滤波器

图7-24为一典型的有源一阶低通滤波器（Active First-order Lowpass Filter），其网络函数为

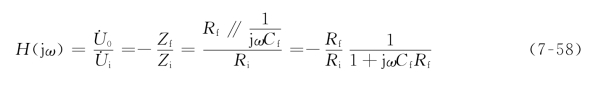
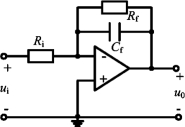
图7-24　有源一阶低通滤波器

式（7-58）和式（7-50）形式基本一样，且有和H（j∞）=0，可见它和无源低通滤波器具有相同的频率响应曲线，只不过还有一个的低频增益或直流增益，其转折频率为

该转折频率与输入阻抗无关，仅由反馈阻抗决定。

2.一阶高通滤波器

对于图7-25所示电路，其网络函数为

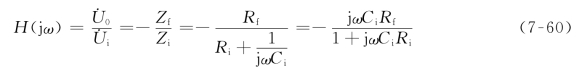
图7-25　有源一阶高通滤波器

式（7-60）和式（7-52）形式基本一样，且有H（j0）=0和，可见它和无源高通滤波器具有相同的频率响应曲线，只不过还有一个的高频增益，其转折频率为

因此，图7-25所示为有源一阶高通滤波器（Active First-order Highpass Filter）。

3.带通滤波器

若将图7-24所示的有源低通滤波器和图7-25所示的有源高通滤波器串接起来，即可构成一个有源带通滤波器（Active Bandpass Filter）。图7-26即为一个单位增益的低通滤波器和单位增益的高通滤波器以及增益为的反相放大器三者级联起来所构成的有源带通滤波器，其网络函数为三者相乘，即

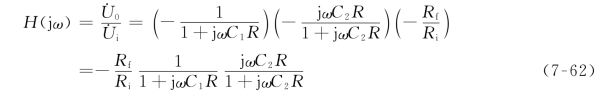
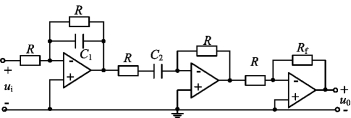
图7-26　有源带通滤波器

第一级为低通滤波器，低通部分设定了带通滤波器的上转折频率

第二级为高通滤波器，高通部分设定了带通滤波器的下转折频率

第三级为反相放大器，它提供增益

带通滤波器的中心频率、带宽和品质因数分别为

4.带阻滤波器

若将图7-24所示的有源低通滤波器和图7-25所示的有源高通滤波器并联再加上一个相加放大器，即可构成一个有源带阻滤波器（Active Bandrejector Notch Filter），如图7-27所示。

其中，带阻滤波器的下转折频率ω1由低通滤波器设定，而上转折频率ω2由高通滤波器设定，ω1和ω2之间的止带是滤波器的带宽。带阻滤波器通过的是低于ω1和高于ω2的频率。

带阻滤波器的网络函数为(www.daowen.com)

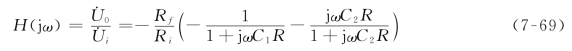
带阻滤波器的中心频率、转折频率、带宽和品质因数与式（7-63）～式（7-68）相同。

例7-14　确定图7-28所示滤波器的类别，并计算其转折频率。若滤波器的输入电压ui中除直流分量外尚有ω=104rad/s的分量。当电路中参数为R=1kΩ，L=1H时，若要求输出电压u0正弦分量占滤波前的5%，问电容C应为多少？

图7-27　有源带阻滤波器

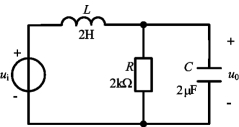
图7-28　例7-14图

解　电路的网络函数为

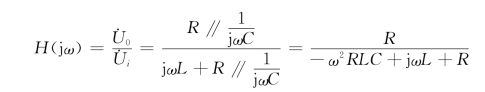
由上式可知，H（j0）=1和H（j∞）=0，因此是一个二阶低通滤波器。其网络函数的模为

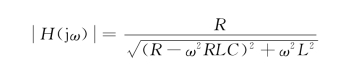
其转折频率就是模下降到其时的半功率频率，即

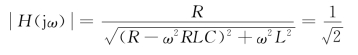
在转折频率处，对上式两边取平方值得

整理得

将R、L和C代入上式得

为方便假设ωC以krad/s计，则上式整理得

解的二次方程，得到，所以有

ωC=0.742krad/s=742rad/s

在R=1kΩ，L=1H时，若要求输出电压u0正弦分量占滤波前的5%，则相当于

代入数值解得

C⋍0.183μF

例7-15　设计一个有源高通滤波器，其高频增益为5，转折频率为2kHz，并取电容值为0.1μF。

解　根据有源高通滤波器的转折频率，有

由有源高通滤波器的高频增益，有

Rf=5Ri=5×796.17=3980.85Ω

取Ri=800Ω，Rf=4kΩ，所设计的高通有源滤波器如图7-25所示.。