为了直观地观察频率特性随频率变化的趋势和特征，需要准确地描绘频率响应曲线。在研究放大电路的频率响应时，由于信号的频率范围很宽，如从几赫到几百兆赫以上，放大电路的放大倍数也很大，如高的可达百万倍。为压缩坐标，扩大视野，在画频率特性曲线时，频率坐标采用对数刻度，即lgω，而幅值响应的幅度值采用分贝（dB）表示，记作，相频响应的相角仍以角度值表示，即0°。这种在对数坐标系中画出的幅频特性和相频特性曲线称为对数频率特性或波特图（BodePlots）。由于波特图采用了对数坐标系，可以在不同频域内用直线近似代替曲线，使曲线局部直线化，整个曲线则折线化，从而使频率响应曲线变得易于描绘，便于表示较大的幅度动态范围和较宽的频率跨度；波特图能将频率特性的绘制与系统函数的极点、零点分布直接联系起来，此外，还可以近似估算系统的频率响应参数，快速了解通带特征。由网络函数绘制出来的对数曲线波特图，现已成为工业生产的标准。

网络函数H（jω）是一个复数，其指数形式为

对其取对数有

其实部为H（jω）的对数模，虚部为H（jω）的相移函数，两者都是ω的实函数。

绘制波特图的方法步骤如下：

第一步：求出电路的网络函数，并对表达式作归一化处理，分析系统的零点、极点和常数项。

第二步：绘制出常数项、实极点、实零点、复共轭极点和复共轭零点等各单项幅频和相频波特图；

第三步：将各个单项线性叠加在一起，即可完整获得系统的幅频和相频波特图。

下面，通过实例来说明绘制波特图的方法和步骤。

例7-12　画出如下网络函数的波特图。

解　第一步，将网络函数作归一化处理，有

因此，对数模和相位分别为

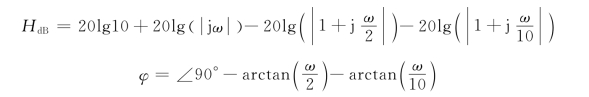
第二步，根据系统的各单项参数，绘制出各单项的幅频波特图和相频波特图，标明转换点及折线斜率。由幅频特性可知。

（1）20lg10=20dB为常量，为20dB的水平直线，如图7-18（a）中的直线①所示。

（2）当ω=0.1时，；当ω=1时，；当ω=10时，。所以为一斜率为20dB的直线，如图7-18（a）中的直线②所示。

（3）当ω→0时，20lg（1）=0；当ω→∞时，。这样，以ω=2为分界点，在ω＜2区间，该项可用斜率为零的直线逼近；在ω＞2区间，该项用斜率为-20dB倍率的直线逼近，因此可由两段直线逼近，如图7-18（a）中的直线③所示。

（4）当ω→0时，20lg（1）=0；当ω→∞时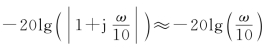，。这样，以ω=10为分界点，在ω＜10区间，该项可用斜率为零的直线逼近；在ω＞10区间，该项用斜率为-20dB倍率的直线逼近，因此可由两段直线逼近，如图7-18（a）中的直线④所示。(www.daowen.com)

第三步，线性叠加出完整的幅频波特图。

将这四项叠加可得幅频波特图，如图7-18（a）中实线所示。

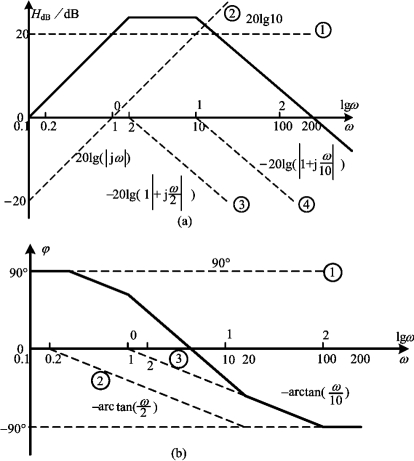
图7-18　例7-12图

（a）幅频波特图；（b）相频波特图

由相频特性可知：

（1）90°为常量，在相频波特图上为水平线，如图7-18（b）中的直线①所示。

（2）当ω=0时，，在0≤ω≤0.2区间，，项可用值为0°的水平直线逼近；当ω=2时，-arctan（1）=-45°；当ω=20时，-arctan（10）=-90°，所以在0.2≤ω≤20区间，项可用斜率为-45°/10倍频的直线逼近；当ω→∞时，，所以，在ω＞20区间，项用值为-90°的水平直线逼近。三段逼近线的交点在ω=0.2和ω=20处，如图7-18（b）中的直线②所示。

（3）类似（2）的分析，可得在1≤ω≤100区间，可用值为0°的水平直线逼近；在ω≥100区间，可用值为-90°的水平直线逼近，如图7-18（b）中③所示。

将以上三条折线叠加可得到相频波特图，如图7-18（b）中实线所示。

例7-13　已知网络函数，画出波特图，根据波特图确定系统的通带特性，并求通带增益和截止频率。

解　第一步，对系统函数作归一化处理，并得出该系统的各单项参数。

由归一化的系统函数可得常数项：K′=20，即26dB；两个实零点为：0，-2；两个负实极点为：-1，-20。

第二步，根据系统的各单项参数，绘制出各单项的幅频波特图和相频波特图，标明转换点及折线斜率。幅频波特图如图7-19（a）中虚线所示，相频波特图如图7-19（b）中虚线所示。

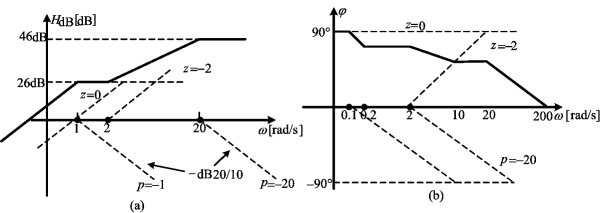
图7-19　例7-13图

（a）幅频波特图；（b）相频波特图

第三步，线性叠加出完整的幅频波特图和相频波特图。

幅频波特图如图7-19（a）中实线所示，相频波特图如图7-19（b）中实线所示。

由幅频波特图可得，该系统为高通系统。截止频率为ω=20rad/s，所以通带增益为