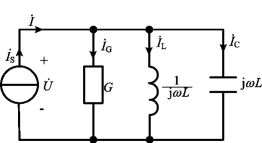
图7-13 GLC并联谐振电路
并联谐振的定义与串联谐振的定义相同,即端口电压![]() 与输入电流
与输入电流![]() 同相位时的工作状况称为谐振。由于谐振是发生在并联电路中,所以称并联谐振。图7-13为RLC并联电路,是与RLC串联电路相对应的另一种形式的谐振电路,分析并联谐振电路方法与RLC串联谐振电路相同。由于并联谐振电路是RLC串联电路的对偶电路,也可利用对偶性质直接得出并联谐振时条件和特性等。
同相位时的工作状况称为谐振。由于谐振是发生在并联电路中,所以称并联谐振。图7-13为RLC并联电路,是与RLC串联电路相对应的另一种形式的谐振电路,分析并联谐振电路方法与RLC串联谐振电路相同。由于并联谐振电路是RLC串联电路的对偶电路,也可利用对偶性质直接得出并联谐振时条件和特性等。
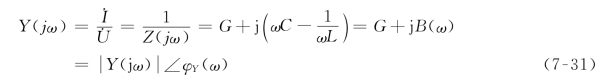
式中,![]() ,
,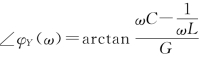
并联谐振条件
lm[Y(jω0)]=0
给合式(7-31),可得谐振时的角频率ω0和频率f0为
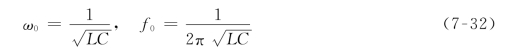
该频率称为电路的固有频率。
并联谐振时,输入导纳Y(jω0)为最小
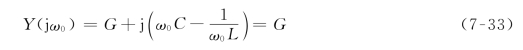
或者说输入阻抗最大,Z(jω0)=R,所以谐振时端电压达到最大值
![]()
可以根据这一现象判别并联电路是否发生了谐振。
并联谐振时有![]() ,所以并联谐振又称电流谐振。
,所以并联谐振又称电流谐振。
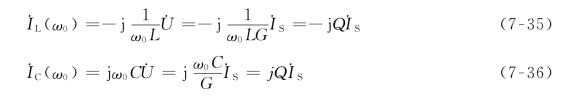
式中,Q——并联谐振电路的品质因数。
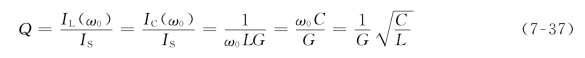
如果Q≫1,则并联谐振时在电感和电容中会出现过电流,但从L、C两端看进去的等效导纳等于零,即阻抗为无穷大,相当于开路。
谐振时无功功率![]() ,QC=-ω0CU2,所以Q=QL+QC=0,表明在谐振时,电感的磁场能量与电容的电场能量彼此相互交换,完全补偿,两种能量的总和为
,QC=-ω0CU2,所以Q=QL+QC=0,表明在谐振时,电感的磁场能量与电容的电场能量彼此相互交换,完全补偿,两种能量的总和为
![]()
并联谐振时半功率点频率为
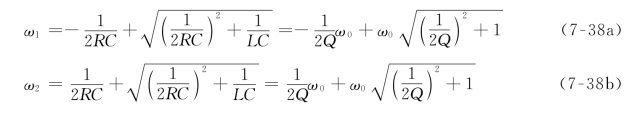
通频带宽BW为
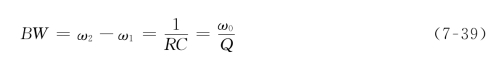
对于高Q电路有
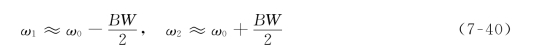
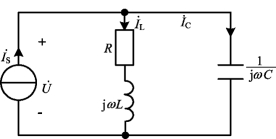
图7-14 实际GLC并联谐振电路
由于实际电感和电容元件都是有损耗的,特别是电感元件的损耗在有些情况下是不能忽略的。因此,对于工程技术中由电感和电容并联组成的谐振电路,其模型常采用图7-14所示电路形式。
在频率为ω的正弦激励电流![]() 作用下,图7-14电路的输入导纳为
作用下,图7-14电路的输入导纳为
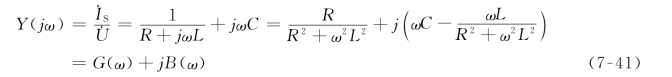
该电路谐振条件
![]()
即有

由此可得电路谐振的角频率ω0和频率f0为
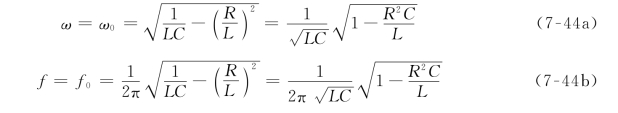
可见,实际并联谐振电路的谐振角频率和频率不仅决定于其电抗元件参数,还与电感线圈的损耗电阻有关。
由于谐振时整个电路等效于电阻,故端口电压![]() 为
为

谐振时电容电流
![]()
谐振时电感电流(www.daowen.com)
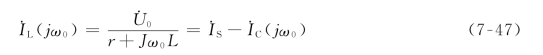
图7-15 例7-9图
例7-9 图7-15所示的RLC并联电路中,已知R=8kΩ,L=0.2mH,C=8μF。
(1)计算ω0、Q和BW;(2)求ω1和ω2;(3)确定ω1、ω2和ω0各处所消耗的功率。
解 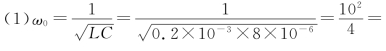
![]()
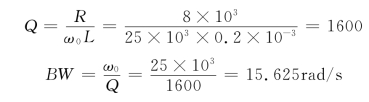
(2)由Q=1600>10,所以是高Q电路,所以有
![]()
(3)ω=ω0时,Z=R=8×103Ω,则
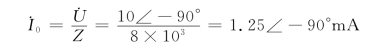
谐振时,全部电流都流过R,所以平均消耗功率为
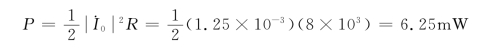
在ω=ω1和ω=ω2时
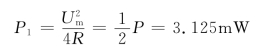
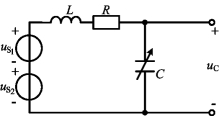
图7-16 例7-10图
例7-10 图7-16所示为某收音机的输入等效电路,已知R=8Ω,L=300μH,C为可调电容。广播电台信号![]()
![]() ,f1=540kHz;
,f1=540kHz;![]() ,f2=600kHz。
,f2=600kHz。
(1)当电路对信号![]() 发生谐振时,求电容C值和电路的品质因数Q。
发生谐振时,求电容C值和电路的品质因数Q。
(2)保持(1)中的C值不变,分别计算![]() 和
和![]() 在电路中产生的电流及电容C上的输出电压。
在电路中产生的电流及电容C上的输出电压。
解 (1)因为![]() ,所以有
,所以有
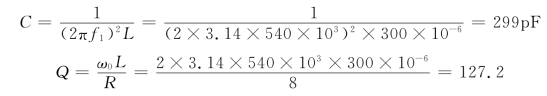
(2)当信号![]() 作用时,电路发生谐振,故
作用时,电路发生谐振,故
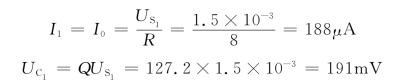
当信号![]() 作用时,电路处于失谐状态,其相对失谐
作用时,电路处于失谐状态,其相对失谐
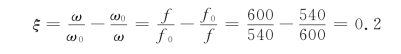
故
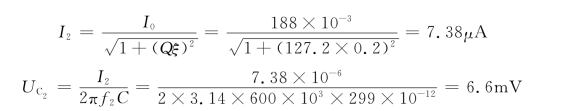
例7-11 图7-17(a)所示为某放大器的等效电路模型。已知US=12V,电源内阻RS=60kΩ,负载电阻RL=60kΩ,L=54μF,C=100pF,r=9Ω,电路对电源发生谐振。求rL-C电路与整个电路的品质因数和通频带。
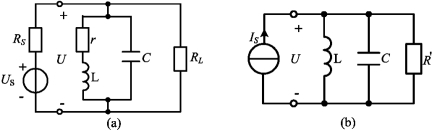
图7-17 例7-11图
解 (1)电路谐振频率
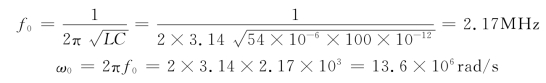
(2)rL-C电路的特性阻抗
ρ=ω0L=13.6×106×54×10-6=734.4Ω
rL-C电路无载品质因数
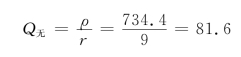
通频带
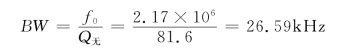
(3)将电压源等效为电流源,把rL-C并联电路等效为RLC并联的等效电路,整理得图7-17(b)所示,其中
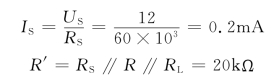
式中,![]() 。
。
整个电路的品质因数和通频带分别为
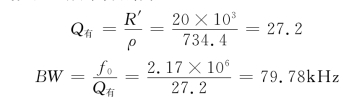
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







