图7-8(a)表示RLC串联电路,它在正弦电压源作用下的相量模型如图7-8(b)所示,其中,电源的频率为ω,则电路的输入阻抗为
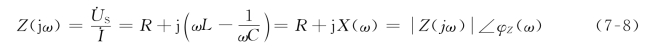
其中
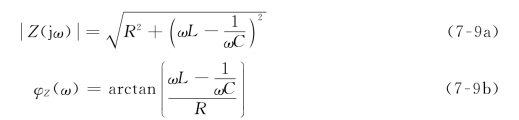
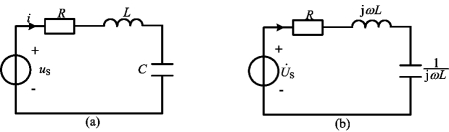
图7-8 RLC串联电路谐振电路
1.谐振条件和谐振频率
假设电路中各元件参数一定,电压源的频率ω可变,根据式(7-8)电路的输入阻抗Z(jω)仅为频率的函数。电路中电阻R、感抗XL=ωL、容抗![]() 、电抗
、电抗![]()
![]() 、阻抗模
、阻抗模![]() 和阻抗角φZ(ω)随频率ω变化的曲线如图7-9所示。
和阻抗角φZ(ω)随频率ω变化的曲线如图7-9所示。
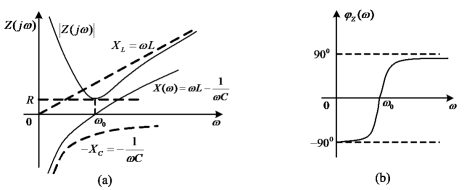
图7-9 RLC串联电路电抗、阻抗随频率变化曲线
(a)电抗、阻抗曲线;(b)阻抗角曲线
由式(7-8)和式(7-9)可知,当![]() ,即
,即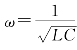 时,有
时,有![]() ,φZ(ω)=0,电压uS与电流i相位相同,电路发生谐振。因此,RLC串联电路的谐振条件为
,φZ(ω)=0,电压uS与电流i相位相同,电路发生谐振。因此,RLC串联电路的谐振条件为

式(7-10)中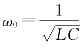 仅由电路自身的元件参数L和C确定,为电路固有的,所以称为电路的固有谐振角频率,简称为谐振角频率,
仅由电路自身的元件参数L和C确定,为电路固有的,所以称为电路的固有谐振角频率,简称为谐振角频率,![]() 称为电路的固有频率(Natural Frequency)。
称为电路的固有频率(Natural Frequency)。
由式(7-10)可知,当RLC串联电路外施激励源的频率与电路本身的固有频率相同时,电路就会发生串联谐振。若电路的元件参数L和C保持为定值,则可调节电源频率使之等于电路自身的谐振频率,使电路发生谐振,称这种调节方法为调频调谐;若保持电源频率不变,通过调整电路参数L或(和)C来改变自身的调谐频率,使之与电源频率相等,从而实现使电路发生谐振,如果调节的是电感,则称调感调谐,如果调节的是电容,则称调容调谐。总之在电感L、电容C和电源角频率ω这三个量中,无论改变哪个参量都可以使电路满足谐振的条件,使之与某一特定频率的信号谐振,这一过程称为调谐。
2.谐振时的电压和电流
RLC串联谐振时电路阻抗的电抗分量X(ω0)=0,所以电路的谐振阻抗为
![]()
即谐振时电路阻抗呈现纯电阻,为其模的最小值R。电感和电容的串联部分对外等效为短路。若在端口上外加电压源![]() ,则谐振时端口电流
,则谐振时端口电流![]() 为
为

可见,电流与电压源电压同相,且达到最大值,称为谐振峰。
谐振时电感和电容的电压分别为
![]()
总电压为
![]()
表明发生串联谐振时,电感电压和电容电压大小相等,相位相反,相互抵消,电感与电容串联部分对外等效于短路,外施电压全部施加于电阻两端,此时的电阻电压也是谐振峰。
3.谐振时的功率和能量
为了方便讨论谐振时电路及各元件的功率,假设电压源电压为uS(t)=USmcos(ω0t),则有

由于谐振时串联回路的端口电流![]() 和电压源电压
和电压源电压![]() 同相位,所以整个电路的功率因数cosφZ0=1,电路吸收的功率为
同相位,所以整个电路的功率因数cosφZ0=1,电路吸收的功率为
![]()
谐振时电感和电容吸收的功率分别为
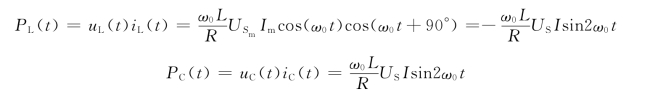
因此,任何时刻进入电感和电容的总功率为零,即PL(t)+PC(t)=0。这说明电源发出的功率全部被电阻吸收。电感和电容之间的能量交换过程如下:
当电流i减小时,电感中磁场能量![]() 减小,所放出的能量全部被电容吸收,并转换为电场能量,如图7-10(a)所示;当电流增加小,电容电压u减小,电容中电场能量
减小,所放出的能量全部被电容吸收,并转换为电场能量,如图7-10(a)所示;当电流增加小,电容电压u减小,电容中电场能量![]()
![]() 减小,所放出的能量全部被电感吸收,并转换为磁场能量,如图7-10(b)所示。能量在电感和电容间往复交换,形成电压和电流的正弦振荡。显然,谐振时电磁场能量的总和之所以能够保持不变,是因为激励电压源在不断地补偿电阻所消耗的能量,这相当于形成了由理想电感和电容元件构成的串联电路,因而所产生的振荡与理想元件L、C电路由初始储能引起的等幅振荡相同,其振荡角频率
减小,所放出的能量全部被电感吸收,并转换为磁场能量,如图7-10(b)所示。能量在电感和电容间往复交换,形成电压和电流的正弦振荡。显然,谐振时电磁场能量的总和之所以能够保持不变,是因为激励电压源在不断地补偿电阻所消耗的能量,这相当于形成了由理想电感和电容元件构成的串联电路,因而所产生的振荡与理想元件L、C电路由初始储能引起的等幅振荡相同,其振荡角频率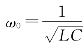 完全由电路参数L和C决定。
完全由电路参数L和C决定。
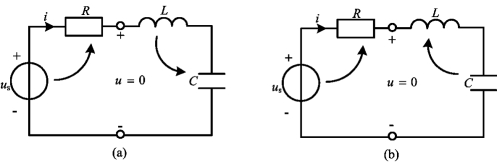
图7-10 RLC串联电路谐振时能量交换
4.品质因数与特性阻抗
由于RLC串联电路的电阻会不断地损耗电能而产生热能,因此,要维持谐振电路中电容与电感之间所进行的同期电磁振荡,电源就必须不断地向电路提供电能,以补偿电阻消耗的那部分能量。显然,如果与谐振时电路中所储存的总电磁能相比,每振荡一次电路所消耗的电能越少,则电路的品质就会越好。为了评价RLC串联谐振电路的品质,定量反映谐振电路的储能效率,在电路理论中引入谐振电路的品质因数这一重要参数,品质因数Q定义为
![]()
由定义式可知,电路的品质因数越大,电容与电感之间交换的参量就越大,电磁振荡的幅度也就越大。
为了方便计算谐振电路的品质因数,总希望建立电路的品质因数与电路参数之间的关系。谐振时RLC电路所储存的总能量
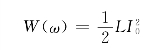
谐振时电路在一个周期内消耗的平均能量为
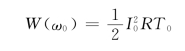
由品质因数定义可得
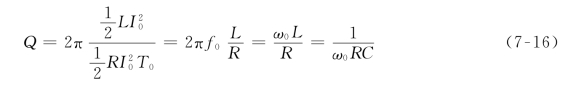
可见,Q值是电路在谐振状态下其感抗或容抗与电阻之比。
将谐振时电路中彼此相等的感抗和容抗定义为谐振电路的特性阻抗,用符号ρ表示,即
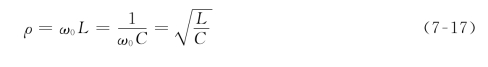
则串联谐振电路品质因数Q与其特性阻抗ρ的关系为

引入品质因数Q后,可以用它来表示谐振时电感电压、电容电压与电源电压之间的大小关系
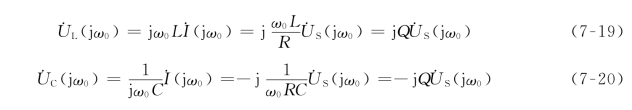
故有
![]()
可见,电感电压和电容电压的大小均为电源电压大小的Q倍,若当Q>1时,则电感和电容两端的电压将分别出现比电源电压高Q倍的过压。因此,串联谐振又称为电压谐振。这种串联谐振时出现的过压,在电路中将产生有利或不利的作用。如在低电压的电路系统中(如无线电接收系统),利用串联谐振时出现的过压来获得较大的输入;而在高电压的电路中(如电力系统),这种过压将会危及系统的安全。
电路的品质因数Q值可通过测定谐振时的电感或电容电压来求得,即

5.RLC串联电路的频率响应
图7-8所示RLC串联电路谐振电路的转移电压比为
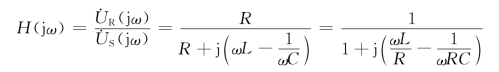
代入![]() ,令
,令![]() ,则上式可改写为
,则上式可改写为
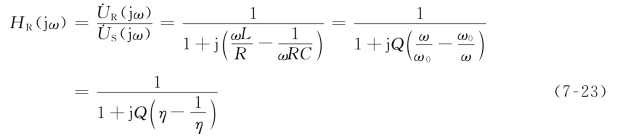
频率响应分别为
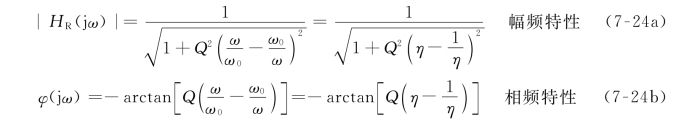
由式(7-24a)可知,当ω=0或ω=∞时,有![]() ;当
;当![]() 时,电路发生谐振,
时,电路发生谐振,![]() 达到最大值,说明该电路具有带通特性,对应的特性曲线如图7-11(a)所示,图7-11(b)给出了不同Q值的幅频特性曲线。因为任何Q值相等的RLC串联电路的频率特性曲线都是相同的,所以,这种曲线又称为串联谐振电路的通用曲线。(https://www.daowen.com)
达到最大值,说明该电路具有带通特性,对应的特性曲线如图7-11(a)所示,图7-11(b)给出了不同Q值的幅频特性曲线。因为任何Q值相等的RLC串联电路的频率特性曲线都是相同的,所以,这种曲线又称为串联谐振电路的通用曲线。(https://www.daowen.com)
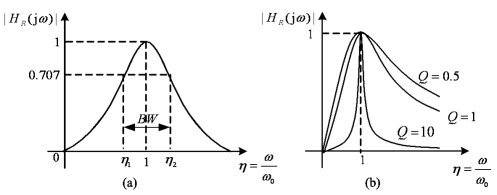
图7-11 RLC串联电路谐振频率特性曲线
根据式(7-24)和图7-11可以看出
在η=1,即谐振点处出现峰值,在其邻域η=1+Δη内有较大幅度的输出信号,当信号的频率偏离谐振频率时,输出信号的幅值从峰值开始下降。这说明RLC串联电路具有在全频域内选择各自谐振信号的性能,但具有带通特性,工程上称这一性能为选择性(Selectivity)。通带限定的频域范围称为通频带宽,记为BW。工程上按下式决定通频带的宽度

式(7-25)取等号,根据式(7-24a)有
![]()
解得
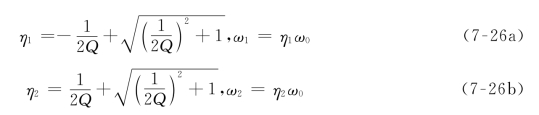
低半功率点频率为
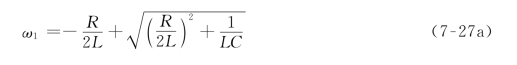
高半功率点频率为
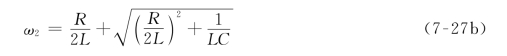
则半功率点频率与谐振频率的关系为
![]()
则通带的频带宽度为
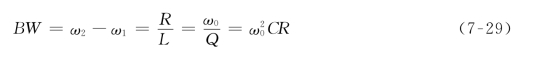
通带的频率范围为
ω1≤ω≤ω2
ω1、ω2分别位于ω0两侧,因此ω0又常称为中心频率,ω1在谐振点左侧,称为下界或下截止频率或低半功率点频率;ω2在谐振点右侧,称为上界或上截止频率或高半功率点频率。
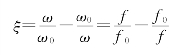 称为相对失谐,表示电路工作频率f对谐振频率f0的相对失谐。
称为相对失谐,表示电路工作频率f对谐振频率f0的相对失谐。
通常谐振电路总是工作在谐振频率处或其邻近处,当电路的品质因数Q≥10时,称为高Q电路(High-QCircuit)。在高Q电路的所有实际应用中,半功率点频率都可认为是对称于谐振频率的,且可近似地按下式表示
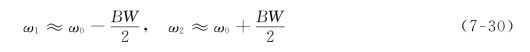
工程上常用通带的带宽BW来比较和评价电路的选择性。由于带宽BW与品质因数Q值成反比,Q值越大,BW越窄,电路选择性越好,抑非能力越强,反之Q值越小,BW越宽,选择性越差,但宽带包含的信号流失少,有利于减少信号的失真。
综上所述,谐振电路可以用以下五个相关的参数来表征:两个半功率点的频率ω1、ω2,谐振频率ω0,带宽BW和品质因数Q。
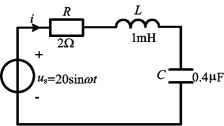
图7-12 例7-7图
例7-7 在图7-12所示的电路中,已知R=2Ω,L=1mH,C=0.4μF。
(1)求谐振频率和半功率点频率;
(2)计算品质因数和带宽;
(3)确定在ω0、ω1和ω2处的电流幅度。
解 (1)谐振频率为
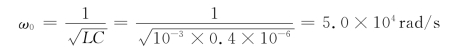
低半功率点频率为
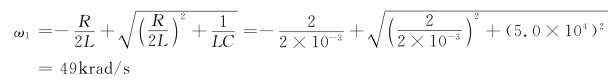
高半功率点频率为
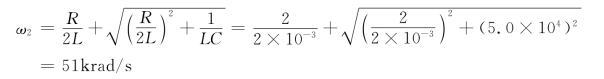
(2)带宽为
BW=ω2-ω1=2krad/s
品质因数为
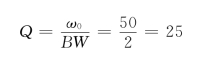
(3)当ω=ω0时,有
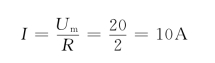
ω=ω1和ω=ω2时,则
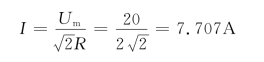
此题还可先求品质因数Q,由Q得到带宽BW,再根据BW求半功率点频率,即
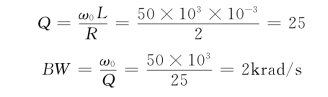
因为Q>10是高品质因数电路,所以半功率点频率为
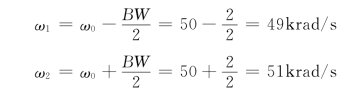
例7-8 RLC串联电路的谐振频率为578Hz,通带宽度为250Hz,已知L=0.32H。
(1)求R、C、品质因数及截止频率;
(2)设输入电压有效值为23.2V,求谐振频率和截止频率时电路的平均功率;
(3)求谐振时电感电压和电容电压。
解
(1)
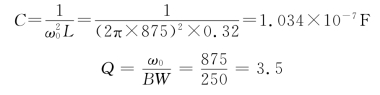
由![]() ,可得
,可得

截止频率分别为
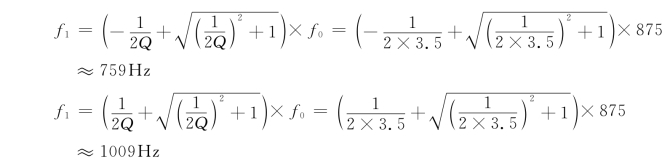
(2)谐振时电路的平均功率为
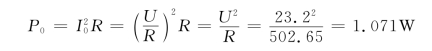
在截止频率处,电流下降至电流I0的![]() ,故功率减小到P0的一半,所以当f1=759Hz和f2=1009Hz时,电路平均功率为
,故功率减小到P0的一半,所以当f1=759Hz和f2=1009Hz时,电路平均功率为
![]()
(3)谐振时电感电压和电容电压相等,为
UL=UC=QU=3.5×23.2=81.2V
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







