正弦稳态网络函数H（jω）是电路自身的一种反映，它决定于电路的结构和参数。由于电路中的感抗和容抗是频率的复函数，所以在电路结构、元件参数值一定的情况下，当指定激励端钮对与响应端钮对时，正弦稳态网络函数与激励的振幅和初相无关，仅为激励源频率ω的复数，且是以频率ω为变量的两个多项式之比，可以表示为

式（7-6）中为正弦稳态网络函数H（jω）的模，它反映了电路响应与激励的幅值之比和频率的关系，称为幅度频率特性，简称幅频特性（Amplitude-frequency Characteristic），即

φ（ω）为正弦稳态网络函数H（jω）的相位，它表明电路响应相量与激励相量的相位差和频率的函数关系，称为相位频率特性，简称相频特性（Phase-frequency Characteristic），即

式（7-7）表征了电路响应与频率的关系，称为电路的频率响应或频率特性（Frequency Characteristic）。

为了直观反映电路的频率特性，可以将幅频特性和相频特性分别画成曲线，称为电路的幅频特性曲线和相频特性曲线，这两种特性曲线合称为频率特性曲线。

例7-5　求图7-6（a）所示RC电路的电压转移函数，并绘出幅频特性曲线和相频特性曲线。若输入电压，求输出电压u2，已知τ=RC=10-3s。

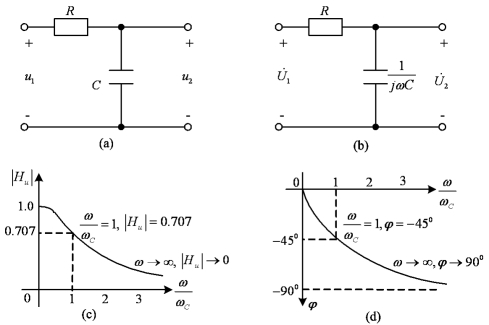
图7-6　例7-5图

解　（1）绘特性曲线。作出图7-5（a）所示RC电路的相量模型如图7-5（b）所示，利用串联电路分压关系可得

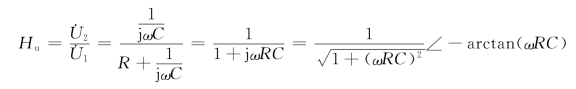
所以有

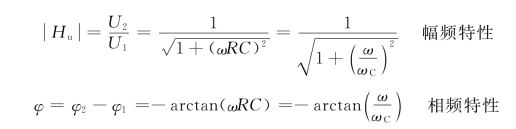
根据以上两式，即可作出幅频特性曲线和相频特性曲线。

由幅频特性可知，当ω=0时，；当ω→∞时，；而当时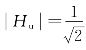，。再计算若干个ω对应的值，即可作出幅频特性曲线，如图7-6（c）所示。由图7-6（c）可得，对于同样的输入电压来说，频率越高，输出电压就越小，在直流时，输出电压最大，恰好为输入电压。因此，低频的正弦信号要比高频的正弦信号更容易通过这一电路。这一电路又称为RC低通电路（Low-pass Circuit）。由于选频电路能够滤除输入中某些频率信号，因此又可称为滤波器或滤波电路，所以低通电路又称低通滤波器（Low-pass Filter）。由于功率与电压的平方成正比，当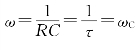时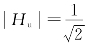，，此时功率将降低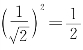，因此，称为半功率点频率（Half Power Point Frequency）。工程技术上把频率从0到ωC的范围定为这一低通滤波器的通频带（Bandwidth，简写作BW），而ωC又称为截止频率（Cut-off Frequency）。(www.daowen.com)

由相频特性可知，随着ω由0向∞趋近，相移角φ单调地趋向-90°，如图7-6（d）所示。相移角φ总为负，说明输出电压总是滞后于输入电压，滞后的角度范围为0°≤φ≤-90°，具体数值取决于ω。因此，这一RC电路又称为滞后网络（Lag Network）。

（2）求输出电压。

当ω=500π=1571rad/s时，由幅频特性得，由相频特性得φ=-57°，所以有

故

例7-6　求图7-7（a）所示RC串联电路电压比，并绘出其频率响应。

解　利用分压关系，有

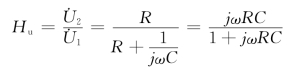
令，则上式改写为

图7-7　例7-6图

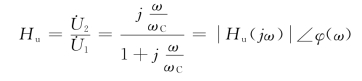
其中

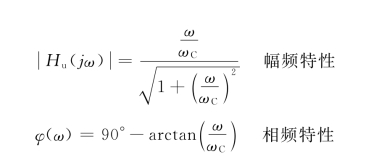
由幅频特性和相频特性关系式即可绘出频率响应曲线如图7-7（b）、图7-7（c）所示。

由图7-7（c）可得，对于同样的输入电压来说，频率越高，输出电压就越大，频率越低，输出电压就越小，在直流时，输出电压最小，为零。因此，高频的正弦信号要比低频的正弦信号更容易通过这一电路。这一电路又称为RC高通电路（Highpass Circuit）或高通滤波器（Highpass Filter）。