电路和系统的工作状态随频率的变化而变化的现象称为电路和系统的频率特性（Frequency Characteristic），又称为频率响应（Frequency Response）。为了研究电路特性与频率的关系，希望定义一个与激励幅值和初相位无关的函数，在输入变量和输出变量之间建立关系来描述电路的频率特性，这一函数关系称为电路和系统的网络函数（Network Function），也称传递函数（Transfer Function）。

电路在一个正弦电源激励下稳定时，电路中各部分的响应（电压或电流）都是同频率的正弦量，我们定义响应相量和激励相量之比称为正弦稳态电路的传递函数或网络函数，记为H（jω），可表示为

式中，为输出端口的响应相量，可为电压相量，也可为电流相量；为输入端口的激励相量，可为电压相量，也可为电流相量。

由于电路中的感抗和容抗都是频率ω的复函数，所以，网络函数H（jω）一般也是频率ω的复函数。由于式（7-1）中响应相量和激励相量在电路中所处的位置可以在同一对端钮上，也可以在不同对端钮上，因此，网络函数的物理意义就不相同。

若响应相量和激励相量在同一对端钮上，此时的正弦稳态网络函数称为驱动点函数或策动点函数（Driving Point Function）。当激励是电流源，响应是电压时，称驱动点阻抗函数；当激励是电压源，响应是电流时，称驱动点导纳函数，如图7-1（a）和（b）所示，于是有

若响应相量和激励相量在不同对端钮上，则此时的正弦稳态网络函数称为转移函数或传输函数（Transfer Function）。如图7-1（c）和（d）所示，于是有

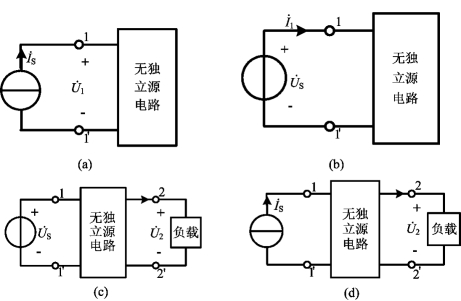
图7-1　正弦稳态电路的传递函数

（a）、（b）驱动点函数；（c）、（d）转移函数

网络函数不仅与电路的结构、参数值有关，还与输入、输出变量的类型以及端钮对的相互位置有关，它是网络性质的一种体现，与输入、输出的幅值无关。网络函数可以用相量法中任一分析方法求得。一般来说，在已知网络相量模型的条件下，计算网络函数可采用外加电源法：在输入端外加一个电压源或电流源，用正弦稳态分析法的任一种方法求出相量的表达式，然后将输出相量与输入相量相比，求得相应的网络函数。对于二端元件组成的阻抗串并联网络，也可以用阻抗串并公式计算驱动点阻抗和导纳，用分压、分流公式计算转移函数。

网络函数H（jω）还可以用多项式的分子N（jω）和分母D（jω）之比来表示

式（7-5）中分子和分母的公因子已经消去了的式子，已经将多项式的比降到最低阶了。多项式N（jω）=0的根称为H（jω）的零点；多项式D（jω）=0的根称为H（jω）的极点。因此，零点是分子多项式的根，它是网络函数的等于零的jω值；极点是分母多项式的根，它是使网络函数等于无穷大的jω值。

在计算H（jω）时，为了方便，临时用s取代jω，即令s=jω，计算完后再用jω替代s。

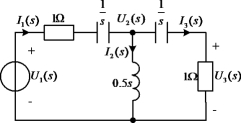
图7-2　例7-1图

例7-1　求图7-2所示电路的电压传输函数。

解　方法一：倒推法。由图7-2电路可知

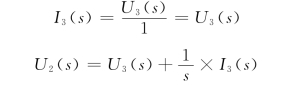
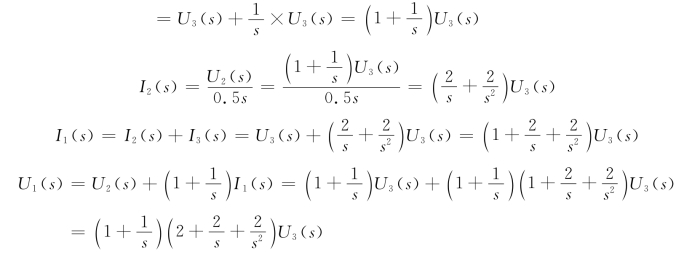
所以有

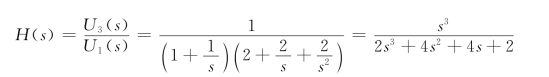
方法二：回路分析法。设图7-2电路左右两回路的电流分别为和，设回路的绕行方向都为顺时针方向，则两回路方程为

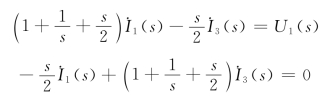
又

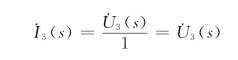
联立求解得(www.daowen.com)

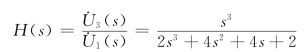
例7-2　图7-3所示电路，已知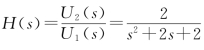，求L和C的值。

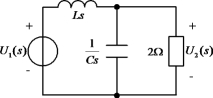
图7-3　例7-2图

解　并联支路总的阻抗为

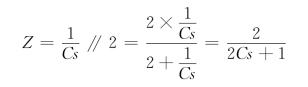
由分压公式可得

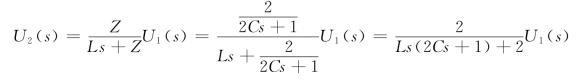
所以有

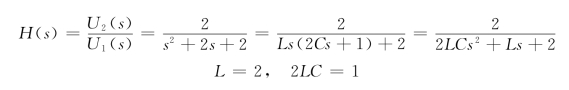
故得

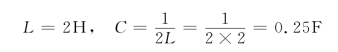
例7-3　求图7-4（a）所示电路的转移电压比。

图7-4　例7-3图

解　先画出相量模型，如图7-4（b）所示。外加电压，列节点方程为

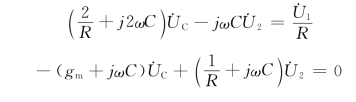
解得

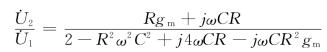
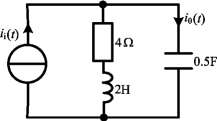
图7-5　例7-4图

例7-4　如图7-5所示电路，计算增益，以及其极点和零点。

解　按分流原理

可得

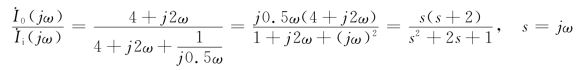
所以，零点为s（s+2）=0，解得

z1=s1=0， z2=s2=-2

极点为s2+2s+1=0，解得

p1=p2=-1

所以，在p=-1处有一个重复极点（或双极点）。