铁芯变压器是常用的器件,在实际中得到广泛应用。在讨论含实际铁芯变压器电路时常常需要将实际铁芯变压器用一定的模型电路来代替,本节讨论它的电路模型问题。
若能认为变压器较好地满足k=1,参数L1、L2为无穷大以及无损耗等理想变压器的理想条件,或对分析要求不高,允许存在相当的误差,就可以将其视为理想变压器,用理想变压器作为模型。如电子设备中的电源变压器,并不需要研究它的频率响应就属于这种情况。详情参看6-5节。
若变压器的耦合系数k=1,无损耗,但耦合线圈的参数值不为无穷大,此时可用全耦合变压器作为其模型,详情参看6-6节。
若无损耗,但耦合系数k<1,参数L1、L2均为有限值,如图6-39(a)所示,图6-39(b)为其电路模型。

图6-39 无损、自感量值有限的非全耦合变压器电路模型
(a)非全耦合变压器示意图;(b)等效电路模型
设电流i1在初级线圈产生的磁通为Φ11,其中主要部分与次级线圈相交链,称为主磁通,记为Φ21,而Φ11中不与次级线圈相交链的部分,记作Φσ1,称为漏磁通,因此有
Φ11=Φ21+Φσ1
类似地有
Φ22=Φ12+Φσ2
由自感系数的定义可知
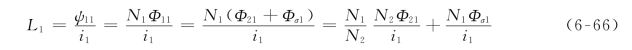 (https://www.daowen.com)
(https://www.daowen.com)
考虑到![]() ,式(6-66)可表示为
,式(6-66)可表示为
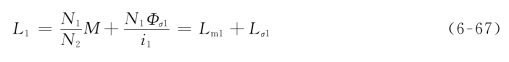
式(6-67)中,![]() 是初级线圈自感中与主磁通相对应的一部分,称为主电感,
是初级线圈自感中与主磁通相对应的一部分,称为主电感,![]() 则是初级线圈自感中与漏磁通相对应的一部分,称为漏电感。
则是初级线圈自感中与漏磁通相对应的一部分,称为漏电感。
同理有

式(6-68)中![]() 是次级线圈自感中与主磁通相对应的主电感,
是次级线圈自感中与主磁通相对应的主电感,![]() 则是次级线圈中漏磁通所对应的漏电感。
则是次级线圈中漏磁通所对应的漏电感。
由于存在漏磁通,两个线圈之间不是全耦合的,但就两个线圈的主磁通而言却是全耦合的。因此,图6-39(a)所示的无损、自感值有限的非全耦合变压器可以等效为由主电感Lm1、Lm2组成的全耦合变压器与初、次级回路各串联漏电感Lσ1、Lσ2的电路,如图6-40(a)所示,再将其中的全耦合变压器等效为励磁电感和变比为n的理想变压器组成的电路,如图6-40(b)所示。
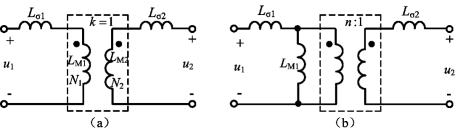
图6-40 无损、自感量值有限的非全耦合变压器的等效电路
(a)含全耦合变压器的等效电路;(b)含理想变压器的等效电路
若耦合系数k<1,参数L1、L2均为有限值,再考虑初、次级线圈电阻损耗以及铁芯的涡流损耗和磁滞损耗,则应在图6-40(b)所示的无损、自感值有限的非全耦合变压器的初、次级分别串联以绕损耗电阻R1和R2,在励磁线圈上并联以铁芯损耗电导G,从而得到三个理想条件均不满足的实际铁芯变压器模型,如图6-41所示。

图6-41 实际铁芯变压器的等效电路
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。





