在图6-28(a)所示理想变压器示意图中,假设Φ11和Φ12分别为初级线圈的自感磁通和互感磁通,对应的自感磁链和互感磁链分别为ψ11和ψ12,Φ22和Φ21分别为次级线圈的自感磁通和互感磁通,对应的自感磁链和互感磁链分别为ψ22和ψ21,则初级线圈的总磁链和次级线圈的总磁链分别为
ψ1=ψ11+ψ12=N1(Φ11+Φ12)
ψ2=ψ22+ψ21=N2(Φ22+Φ21)
在理想情况下为全耦合,即k=1,所有磁通和两个绕组耦合,则有Φ12=Φ22,Φ21=Φ11,因此可设Φ=Φ11+Φ12=Φ22+Φ21,称为互磁通(Mutualflux)或主磁通,它既穿越初级线圈,也穿越次级线圈。
根据法拉第电磁感应定律,可得主磁通中通过初级和次线圈分别产生的感应电压为

将式(6-42)和式(6-43)相比得
![]()
式(6-44)表明,在图6-28(a)所示的理想变压器的初、次级线圈中,由主磁通产生的感应电压在同名端处的极性总是相同,当u1、u2的参考极性的“+”极性端设在同名端,则u1、u2同号,所以初、次级线圈电压之比等于初线圈匝数N1和次级线圈匝数N2之比。
若u1、u2的参考方向的“+”极性端设在异名端,则u1、u2异号,这时u1与u2之比等于负的N1和N2之比,即

式(6-44)和式(6-45)称之为理想变压器的变压关系式。
根据安培环路定律,沿闭合回线l磁场强度H的线积分等于包围在此闭合曲线内的电流的代数和,即
![]()
由于在理想条件下,磁导率μ→∞,故有![]() ,因此有
,因此有
N1i1+N2i2=0
所以有

式(6-46)表明,当初、次级电流i1和i2的参考方向分别同时从同名端流入(或同时流出)时,电流i1和i2之比等于匝数比的负倒数。
同理可求得,当初、次级电流i1和i2的参考方向分别同时从异名端流入(或同时流出)时,电流i1和i2之比等于匝数比的倒数,即
![]()
式(6-46)和式(6-47)称之为理想变压器的变流关系式。
综上所述,在图6-29(a)所示同名端和参考方向下,理想变压器的伏安关系为

在图6-29(b)所示同名端和参考方向下,理想变压器的伏安关系为

式(6-48)的相量形式为
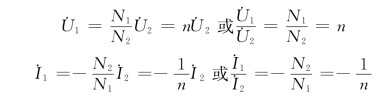
根据图6-29以及式(6-48)和式(6-49),可总结如下规律:
(1)不论初、次级线圈电流的参考方向如何,当初、次级线圈端口电压参考方向的极性位于同名端时,联系初、次级线圈电压方程中的变比n前取“+”号;否则取“-”号。
(2)不论初、次级线圈电压的参考方向如何,当初、次级线圈端口电流参考方向都是从同名端流入(或流出)时,联系初、次级线圈电流方程中的变比n前取“-”号;否则取“+”号。
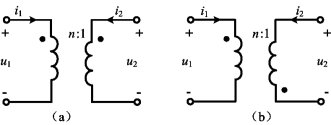
图6-29 理想变压器及其伏安关系
由理想变压器的特性方程式(6-48)可以得出如图6-30(a)所示的理想变压器模型,其受控源表示的等效电路如图6-30(b)、(c)所示。
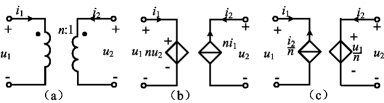
图6-30 理想变压器受控源等效电路
(a)理想变压器;(b)、(c)受控源等效电路
理想变压器不仅能改变电压和电流,而且也能改变阻抗,是一种阻抗变换器。在工作于正弦稳态下的理想变压器的次级线圈接上复阻抗ZL时,如图6-31(a)所示,从初级看进去的等效输入复阻抗为
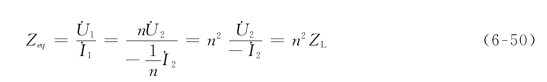
式(6-50)中应用了![]() ,因为在图6-31(a)中,复阻抗ZL上电压与电流参考方向为非关联,称为理想变压器的阻抗变换关系。习惯上把输入阻抗Zeq称为次级对初级的折合阻抗,即阻抗为ZL的负载接在理想变压器的次级,相当于在初级接上一个Zeq=n2ZL的阻抗,如图6-31(c)所示。
,因为在图6-31(a)中,复阻抗ZL上电压与电流参考方向为非关联,称为理想变压器的阻抗变换关系。习惯上把输入阻抗Zeq称为次级对初级的折合阻抗,即阻抗为ZL的负载接在理想变压器的次级,相当于在初级接上一个Zeq=n2ZL的阻抗,如图6-31(c)所示。
同理,当理想变压器初级接有负载阻抗ZL,如图6-31(b)所示,则从次级端口看进去的等效阻抗为

由式(6-50)可知,阻抗变换作用只改变了阻抗的大小,不改变阻抗的性质,并且这种变换性质与电压、电流的参考方向无关,即与同名端的位置无关。若ZL=0,则Zeq=0;若ZL=∞,则Zeq=∞。这表明理想变压器次级短路则初级也短路;理想变压器次级开路则初级也开路。若理想变压器次级短路,将会使初级电流很大,造成线圈过热,导致烧毁变压器设备,因此,在实际应用中必须防止变压器次级短路。
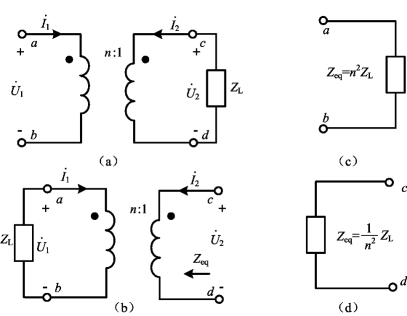
图6-31 理想变压器阻抗变换
在任意时刻t,理想变压器吸收的功率为
![]()
这表明,从初级进入理想变压器的功率全部传输到次级负载上,理想变压器自身既不储存能量,也不消耗能量,在电路中只起传递信号和能量的作用。(https://www.daowen.com)
由于理想变压器的伏安关系是线性函数关系,又是代数关系,因此理想变压器是线性元件和记忆元件。
对于含理想变压器元件电路,可以采用变压器等效电路法、回路法或网孔法、节点法和戴维南定理法等方法分析计算。变压器等效电路法就是先求理想变压器初级等效电路和次级等效电路,然后分别对两个等效电路求解;回路法或网孔法通常是先将理想变压器初级、次级绕组视为一个电压未知的电压源,以其未知电压变量参与列写回路或网孔方程,然后再补充理想变压器电压、电流特性方程,最后联立求解所列写的回路或网孔方程与理想变压器特性方程;节点法是将理想变压器初级、次级绕组视为一个电流未知的电流源,以其未知电流变量参与列写节点方程,然后再补充理想变压器电压、电流特性方程,最后联立求解所列写的节点方程与理想变压器特性方程;戴维南定理法先要求得开路电压,再求等效阻抗,得到戴维南等效电路,然后求解。下面通过实际来说明各种方法的应用。
例6-15 电路如图6-32(a)所示,已知RL=50Ω,试求电压![]() 。
。
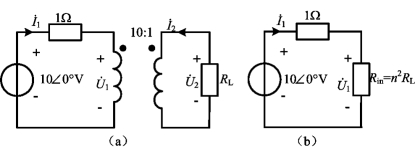
图6-32 例6-15图
解 方法一:采用变压器等效电路方法求解。次级电阻在初级折合电阻为
Rin=n2RL=102×50=5×103Ω
得初级等效电路如图6-31(b)所示。由此可得
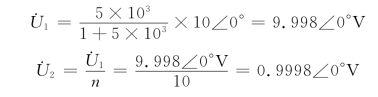
方法二:采用网孔分析法求解
设图6-32(a)所示电路的网孔电流分别为![]() 和
和![]() ,理想变压器的端电压分别为
,理想变压器的端电压分别为![]() 和
和![]() ,列写网孔电流方程为
,列写网孔电流方程为
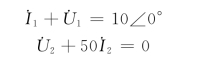
根据理想变压器伏安关系有
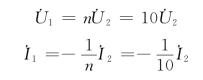
联立求解上述4个方程得
![]()
例6-16 在图6-33所示正弦稳态电路中,试求4Ω电阻消耗的有功功率。

图6-33 例6-16图
解 采用节点法求解
以接地点为参考节点,设节点①、②、③电压分别为![]() 、
、![]() 、
、![]() ,由图可知
,由图可知
![]()
对节点①、②、③列写节点方程
节点①
![]()
节点②
![]()
节点③
![]()
根据理想变压器的电压、电流关系式有
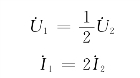
联立求解以上5个方程,可求得
![]()
故4Ω电阻消耗的有功功率为
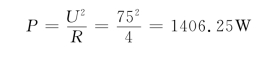
例6-17 电路如图6-34(a)所示,ω=100rad/s,求Z为何值时能获得最大功率Pmax,Pmax的值为多少?
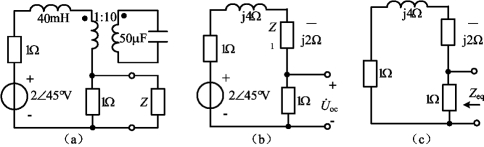
图6-34 例6-17图
解 采用戴维南定理法求解
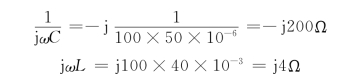
次级阻抗折合到初级为
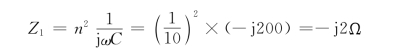
将阻抗Z开路,即得到初级等效电路如图6-34(b)所示,根据该电路求端口开路电压![]()
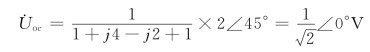
根据图6-34(c)所示电路求端口的等效阻抗Zeq
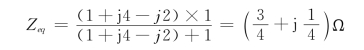
根据最大功率传输定理,当![]() 时,Z能获得最大功率Pmax
时,Z能获得最大功率Pmax
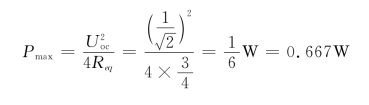
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







