耦合电感元件的两耦合线圈间不仅存在着磁的耦合，而且还有电流的直接联系，即耦合电感的各线圈电流满足线性相关的KCL方程。当有耦合的各线圈电流之间没有直接联系，线圈的电流、电压仅由磁耦合而产生，则称具有这种特性的典型电路就是变压器（Transformer）。

变压器是一种利用磁耦合原理实现能量或信号传输的多端电路器件。实际变压器分为铁芯变压器（Iron-core Transformer）和空心变压器（Air-core Transformer）两种。铁芯变压器是由两个绕在同一磁导率很高的铁磁材料制成的芯子上并具有互感的线圈组成的，因而是耦合系数接近1的紧耦合互感元件，一般说来，这种变压器的电磁特性是非线性的，故以属于非线性变压器（Nonlinear Transformer）。空心变压器是由两个绕在非铁磁材料制成的芯子（有的就以空气为芯）上并具有互感的线圈组成的，因为这种变压器的电磁特性是线性的，故也称线性变压器（Linear Transformer）。铁芯变压器属于紧耦合，在电力工程中主要用于高、低电压的转换，而在电子技术中主要起阻抗变换作用；空心变压器的耦合系数小，属于松耦合，但因其没有铁芯中的各种功率损耗，所以常用于高频、甚高频等电子电路中。本节讨论含空心变压器电路的分析方法。

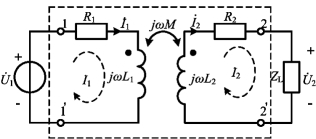
图6-24　空心变压器电路的相量模型

空心变压器可用一对耦合电感作为电路模型，计及绕组铜耗的空心变压器简化电路模型如图6-24所示，其中虚线框内的部分即为空心变压器的电路模型。通常和电源相连接的绕组称为初级线圈或一次绕组，也称为变压器的原边（First Windings），和外接负载相接的绕组称为次级线圈或二次绕组，亦称为变压器的副边（Secondary Windings）。R1和R2分别代表初级线圈和次级线圈的铜耗等效电阻。

在图6-24所示的正弦稳态电路中，假设各元件上的电压与电流的参考方向相关联，则由KVL可得

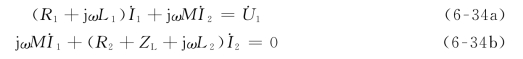
若令Z11=R1+jωL1=R11+jX11，称为初级回路的自阻抗；Z22=R2+ZL+jωL2=R22+jX22，称为次级回路的自阻抗；Z12=jωM反映耦合电感次级回路对初级回路影响的互阻抗，而Z21=jωM反映耦合电感初级回路对次级回路影响的互阻抗。则式（6-34）可写成一般式

可见，只要确定初级回路和次级回路的自阻抗和互阻抗，就可通过列出初级和次级回路方程，而求得初、次级电流以及电路中的电压或功率。

由式（6-35）可求得

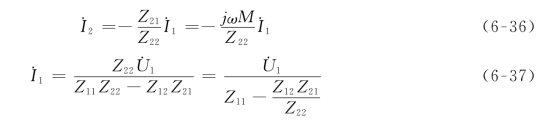
式（6-37）中，无论Z12=Z21为jωM或-jωM，均有-Z12Z21=-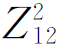=-=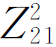ω2M2，因此式（6-37）可以改写为

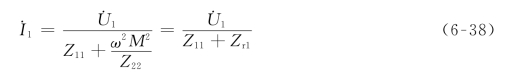
式中，。由式（6-38）可得初级回路的等效电路（Primary Equivalent Circuit）如图6-25（a）所示。根据输入阻抗的定义，初级回路输入阻抗为

式（6-39）说明，初级回路的输入阻抗可以分为两部分，第一部分为初级回路自身的阻抗Z11，即无互感时的阻抗Z11=R1+jωL1=R11+jX11，第二部分为次级回路自阻抗Z22通过由互感耦合作用反映到初级回路的等效阻抗Zl，称为次级回路对初级回路的反映阻抗。考虑到Z22=R22+jX22，有

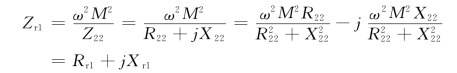
式中，称为次级回路对初级回路的反映电阻，即引入电阻，因为，即反映电阻恒为正，所以次回路自电阻R22反射到初级时仍然是电阻，仅数值的大小发生了改变；

称为次级回路对初级回路的反映电抗，即引入电抗，由该式可知，次级回路自电抗X22反向到初级回路时，不仅数值发生了改变，且性质也发生改变。即当X22＞0，为感性，则Xr1＜0，为容性；而当X22＜0，为容性，则Xr1＞0，为感性。这说明引入电抗与次级回路电抗的性质相反。

将式（6-38）代入式（6-36）可得

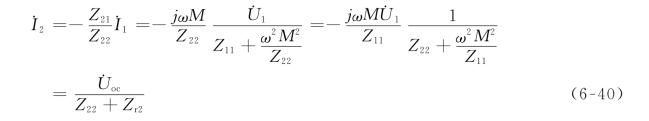
由式（6-40）可得次级回路的等效电路（Secondary Equivalent Circuit）如图6-25（b）所示。

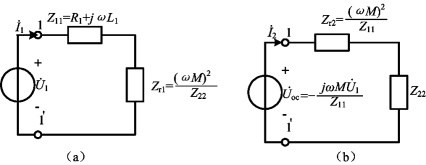
图6-25　空心变压器等效电路

（a）初级回路等效电路；（b）次级回路等效电路

式（6-40）中，为初级回路对次级回路的反映阻抗，其中称为初级回路对次级回路的反映电阻，称为初级回路对次级回路的反映电抗，Z22+Zr2称为次级回路总等效阻抗；为2-2′端的开路电压，即电感L2上的互感电压，其参考方向与的相反，称为次级引入电压。

综上所述，引入反映阻抗概念后，空心变压器所代表的双回路耦合电路的计算可转化为对所建立的初级回路等效电路和次级回路等效电路两个单回路的计算，而不必列方程组计算。

例6-13　空心变压器电路如图6-26（a）所示，已知L1=3.6H，L2=0.06H，M=0.465H，R1=20Ω，R2=0.08Ω，RL=42Ω，uS（t）=115cos（314t）V，求i1和i2。

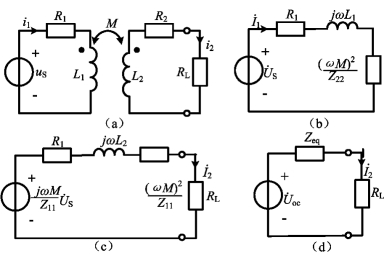
图6-26　例6-13图

解　（1）用初级回路等效电路求i1。图6-26（a）电路的初级回路等效电路如图6-26（b）所示，根据题意有

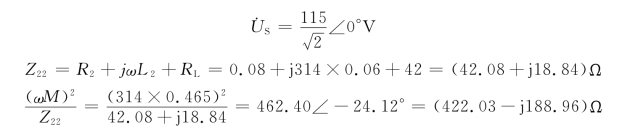
故(www.daowen.com)

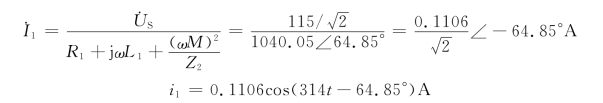
（2）用次级回路等效电路求i2。次级回路等效电路如图6-26（c）所示，图中

Z11=R1+jωL1=20+j314×3.6=（20+j1130.4）Ω

则初级回路向次级回路的反映阻抗为

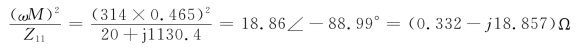
故图6-26（c）所示电路的戴维南等效电路的开路电压和等效阻抗分别为

由此可得到图6-26（d）所示电路的戴维南等效电路，由该等效电路即可求得电流为

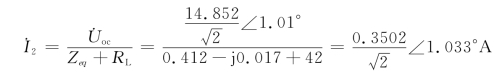
故

i2=0.3502cos（314t+1.033°）A

例6-14　空心变压器电路如图6-27（a）所示，求电路中的和。

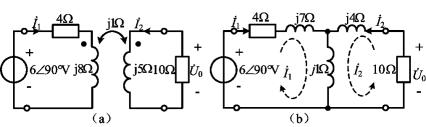
图6-27　例6-14图

解　对于空心变压器，可采用反映阻抗法来分析

初级回路的反映阻抗为

初级回路的电流为

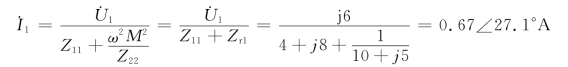
次级回路的戴维南等效电压为

戴维南等效阻抗为

次级回路的电流为

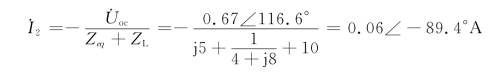
负载上的电压为

此题还可以利用去耦等效法来求解，其去耦等效电路如图6-27（b）所示，由等效电路可列写网孔方程为

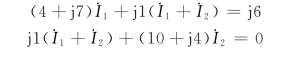
联立求解得

负载上的电压为