【摘要】:图6-4推导耦合电路中存储能量表达式电路如图6-4所示的电路,假设初始时电流i1和i2均为零,则初始时线圈中的储能为零。现令i1由0增加到I1,并维持i2=0,则线圈1中的功率为:其储存的能量为现在维持i1=I1,并将i2从0增加到I2,则在线圈1中的互感电压为,因为I1没有变化,在线圈2中的互感电压为零。
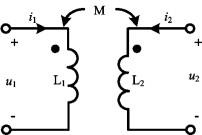
图6-4 推导耦合电路中存储 能量表达式电路
如图6-4所示的电路,假设初始时电流i1和i2均为零,则初始时线圈中的储能为零。现令i1由0增加到I1,并维持i2=0,则线圈1中的功率为:
![]()
其储存的能量为
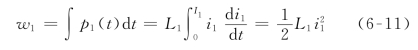
现在维持i1=I1,并将i2从0增加到I2,则在线圈1中的互感电压为![]() ,因为I1没有变化,在线圈2中的互感电压为零。因此,此时两线圈中的功率为
,因为I1没有变化,在线圈2中的互感电压为零。因此,此时两线圈中的功率为
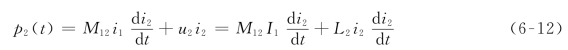
则储存在电路中的能量是
![]()
当i1和i2都到达常量时,线圈中储存的总能量为(https://www.daowen.com)

若将上述分析的电流达到终端的次序换过来,即先是i2从0增加到I2,后是i1从0增加到I1,则线圈中储存的总能量为

因为不管怎样达到最终的条件,电路所储存的能量总是一样的,所以,比较式(6-14)和式(6-15),得到结论
![]()
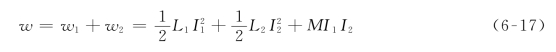
式(6-16)和式(6-17)是在假设两个线圈电流都是流入同名端条件下推导出来的,如果一个电流是流入一个同名端,另一个电流是离开另一个同名端,则互感电压是负的,由此互感MI1I2也是负的,在此情况下,有
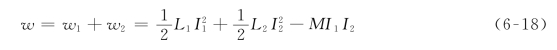
由于I1和I2是任意值,可以用i1和i2取代,这样就得到了电路中储存的瞬时能量的一般表达式
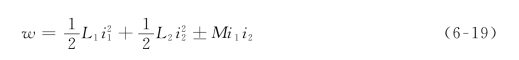
其中,若两个电流都是流入或者离开线圈的同名端,则式中的符号取“+”,否则取“-”号。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章






