为了便于分析，先考虑图6-1所示的两个实际磁耦合线圈，其中L1和L2为两个磁耦合线圈的自感系数，M12和M21分别为两个耦合线圈的互感系数。

图6-1　两线圈的互感作用

（a）自感与互感磁通方向一致；（b）自感与互感磁通方向相反

在图6-1中Φ11和Φ22分别为电感L1和电感L2自身电流i1和i2产生的自感磁通；Φ12为电感L2的电流i2在电感L1中产生的互感磁通，Φ21为电感L1的电流i1在电感L2中产生的互感磁通；N1和N2分别是两线圈的匝数。

若自感和互感磁通方向一致，如图6-1（a）中所示，则两线圈的磁链ψ1和ψ2分别为

式中，ψ11=N1Φ11，ψ22=N2Φ22——线圈1和线圈2的自感磁链；

ψ12=N1Φ12，ψ21=N2Φ21——线圈1和线圈2的互感磁链。

此时，由于电流i1产生的磁通Φ1=Φ11+Φ21和电流i2产生的磁通Φ2=Φ22+Φ12的方向相同，在每个线圈中都是相互增强的，所以互感磁链在叠加时前面取正号。设每个线圈上的端电流和端电压都取关联参考方向，且每个电感中电流的方向和自感磁通的方向符合右手螺旋定则，则根据法拉第电磁感应定律有

式中，——线圈1和线圈2的自感电压；

，——线圈1和线圈2的互感电压。

对于线性时不变的耦合线圈来说，磁链是电流的线性函数，即有ψ11=L1i1，ψ22=L2i2，ψ12=M12i2=Mi2，ψ21=M21i1=Mi1，则式（6-1）可改写为

式（6-3）即为由图6-1（a）所示的两个耦合线圈抽象出的线性时不变耦合电感元件的韦安特性方程，它说明两个线性时不变电感组成耦合电感元件后，作为一个整体必须用L1、L2和M三个参数来描述。将式（6-3）代入式（6-2）中，即可得到耦合电感的伏安特性方程为

式（6-4）说明，每个互感元件上的电压除了决定于本线圈的电流外，还与其他相邻线圈上的电流有关，因此，每个元件上的电压是其自感电压和互感电压的叠加。

若自感和互感磁通方向相反，如图6-1（b）中所示，则两线圈的磁链ψ1和ψ2分别为

(www.daowen.com)

根据法拉第电磁感应定律（Law of Electromagnetic Equation）有耦合电感的伏安特性方程为

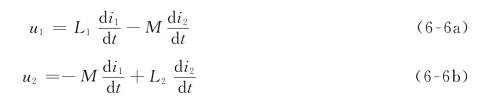
综合式（6-4）和式（6-6）耦合电感的伏安特性方程可用式（6-7）表示

其对应的正弦稳态的伏安关系相量形式为

对自感电压，当u，i取关联参考方向，u，i与Φ符合右手螺旋定则，其表达式为：

式（6-9）说明，对于自感电压由于电压电流为同一线圈上的，只要参考方向确定了，其数学描述便可容易地写出，可不用考虑线圈绕向。

对互感电压，因产生该电压的电流在另一线圈上，因此，要确定其符号，除了知道两耦合电感电流的方向外，还必须知道两个线圈的绕向，由于实际线圈往往是密封的，无法看到具体情况，所以，根据磁通的方向来确定互感电压的正负在实际中是行不通的。为解决这个问题，在电路理论中引入同名端的概念，采用同名端规则来简化这个问题。

若电流i1和i2分别同时从两耦合电感元件的某两个端钮流入（或流出），使其互感磁链与自感磁链的参考方向相同，即两个电流所产生的磁通是相助的，则该两端钮称为耦合电感的同名端（Dotted Terminals），通常用“·”号（“*”号或“△”号）表示。显然，不标记号的一对端钮也是同名端，而一线圈中标记有记号的端钮与另一线圈中无标记的端钮称为异名端。同名端也可表述为，两耦合电感元件中的一个电感元件电流的流入端与由该电流在另一电感元件上所产生的互感电压的参考方向的正极性端，称为同名端。

同名端的规则（The Dot Convention）：若电流进入一个线圈的同名端，则在第二个线圈的同名端处，其互感电压的参考极性是正的。若电流离开一个线圈的同名端，则在第二个线圈的同名端处，其互感电压的参考极性是负的。

用同名端和同名端规则一起就可以确定互感电压的极性。图6-2说明了同名端规则应用于互耦线圈的情况。图6-2（a）所示耦合线圈，互感电压u2的符号取决于电压u2的参考极性和电流i1的方向。由于电流i1是进入线圈1的同名端，且线圈2同名处的电压u2为正，所以互感电压为。在图6-2（b）所示耦合线圈中，电流i1也是进入线圈1的同名端，但电压u2在线圈2的同名端处为负，所以，互感电压为。同理也可得到图6-2（c）和图6-2（d）中的互感电压u1。

图6-2　同名端规则应用示例

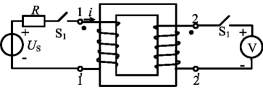
图6-3　同名端的实验测定原理图

同名端也可通过实验测定。图6-3为同名端实验测定原理图，基本原理为：当闭合开关S1时，i增加，有，，所以电压表正偏。当两组线圈装在黑盒里，只引出四个端线钮，要确定其同名端，就可以利用上面的结论来加以判断。