在电子及通信系统中,主要考虑的是如何能够将最大的功率传输给负载。在第三章曾讨论过最大功率传输问题,得到由线性一端口电路传递给可变负载RL的功率最大的条件是:负载RL应与线性一端口电路的戴维南或诺顿等效电阻相等。那么对于正弦稳态电路,负载阻抗满足什么样的条件才能从给定的电源中获得最大的功率?
图5-35(a)为一带负载ZL的正弦稳态电路,图5-35(b)为其对应的戴维南等效电路。负载在一般情况下为阻抗,如电动机、电视天线等。戴维南等效阻抗Zeq和负载阻抗ZL的直角坐标表示为
Zeq=Req+jXeq, ZL=RL+jXL
流过负载的电流为
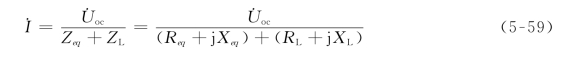
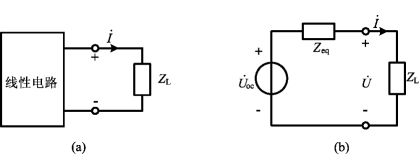
图5-35 最大功率传送条件
(a)带负载的电路;(b)戴维南等效电路
传到负载上的平均功率为
![]()
为求得最大功率传送条件下的RL和XL,令![]() 和
和![]() 。由式(5-60)得
。由式(5-60)得
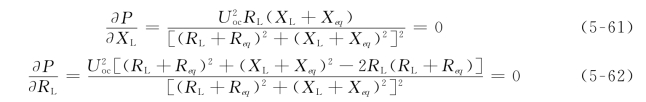
由式(5-61)可得
![]()
由式(5-62)可得
![]()
综合考虑式(5-63)和式(5-64),负载阻抗获得最大功率的条件为
![]()
这时负载获得的最大功率为

该式正是含源二端电路可能提供的最大功率。
综上所述,共轭匹配(Conjugate Matching)时最大功率传递定理(Maximum Average TransferTheorem)为:如果含源二端电路固定而负载任意可调,则负载获得最大功率的条件是负载阻抗为含源二端电路的戴维南等效阻抗的共轭,即
![]()
负载获得的最大功率为含源二端电路可提供的最大功率,即
![]()
显然,第三章中所讨论的电阻电路的最大功率传递定理是现在这一定理的一种特殊情况。
例5-21 图5-36(a)所示电路,求Z为何值时能获得最大功率Pm,Pm的值多大?
解 首先利用戴维南定理求得端口ab左端电路的等效电路,然后利用最大功率传输定理求获得最大功率的条件和最大功率值。
(1)求开路电压
求开路电压的等效电路如图5-36(c)所示,由图可得开路电压为
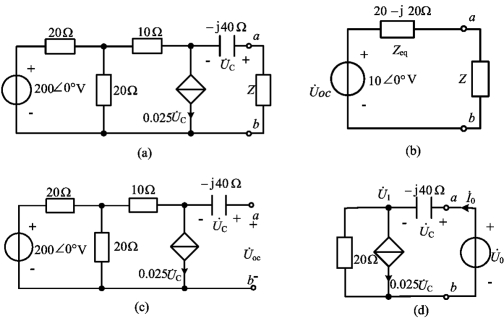
图5-36 例5-21图
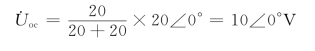
(2)求等效阻抗(https://www.daowen.com)
等效阻抗采用阻抗定义求解,此处采用加电压源求电流的方法求解。电路如图5-36(d)所示断开负载Z,在ab端口加上电压源![]() ,设端口电流为
,设端口电流为![]() ,利用节点分析法,有
,利用节点分析法,有
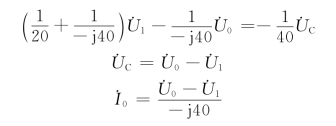
联立以上三式可求得
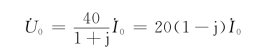
所以,等效阻抗
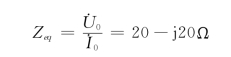
所求得的戴维南等效电路如图5-36(b)所示。故得,当![]() 时,负载Z获得的功率为最大,最大功率为
时,负载Z获得的功率为最大,最大功率为
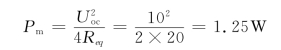
例5-22 图5-37(a)所示电路,已知ω=103rad/s,ZS=RS+jXS=50+j100Ω,R=100Ω,US=100V,现手头只有电容器,试求在R与电源之间连接一个什么样的电路,才能使R获得最大功率Pm,画出电路图,并求出元件的值和Pm的值。
解 因为ZS=RS+jXS=50+j100Ω,R=100Ω,故为使R获得最大功率,应先给R并联一个电容C1,如图5-23(b)所示,则
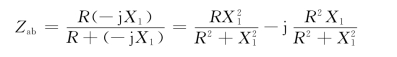
式中,![]() 。今使
。今使
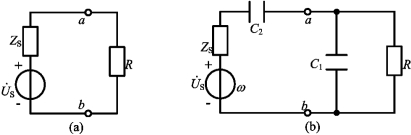
图5-37 例5-22图
![]()
可求得X1=100Ω,又得C1=100μF
为了使R获得最大功率Pm,就必须使![]() ,故应串联一个电容C2,如图5-23(b)所示,并使
,故应串联一个电容C2,如图5-23(b)所示,并使![]() ,故解得X2=50Ω。进而又得
,故解得X2=50Ω。进而又得![]() ,故得C2=20μF。所以
,故得C2=20μF。所以
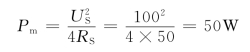
例5-23 图5-38(a)所示正弦电路,其中电源电压有效值US=1V,角频率ω=1rad/s。试求负载获得最大功率时的负载值ZL和获得的最大功率Pmax。
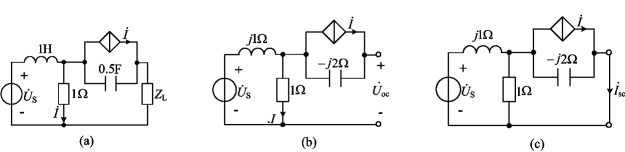
图5-38 例5-23图
解 应用戴维南定理求解。设![]() ,由图5-38(b)所示电路求开路电压
,由图5-38(b)所示电路求开路电压![]()
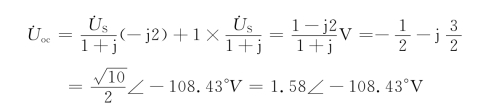
其端口的短路电路![]() 可由5-38(c)所示电路求得,节点电压
可由5-38(c)所示电路求得,节点电压![]() 满足下面方程
满足下面方程
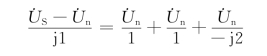
整理得
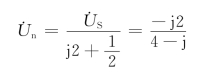
所以,端口的短路电路![]() 为
为
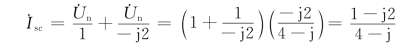
等效阻抗为
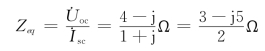
当![]() 时,可获得最大功率为
时,可获得最大功率为
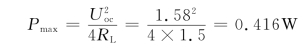
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







