为了能够直接利用任意一端口电路的端口电压相量和电流相量同时计算该电路的有功功率、无功功率、视在功率以及功率因数，可以将参考方向关联的电压相量和电流相量的共轭复数的乘积定义为该一端口电路吸收的复数功率，简称复功率（Complex Power），由表示，即

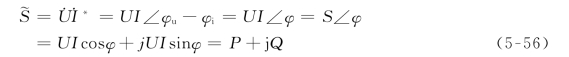
可见，复功率可以将有功功率P、无功功率Q、视在功率S以及功率因数角φ联系起来。在直角坐标下，复功率的实部和虚部分别为有功功率和无功功率；在极坐标下，复功率的模是视在功率，其幅角是功率因数角。复功率的单位与视在功率的单位相同，也是伏安（V·A）。

由于式（5-56）表示的是一个复数，因此，其中用表示的P、Q、S和φ之间的关系可以通过几何图形表示出来，如图5-30所示，称之为功率三角形（Power Triangle），这是一个由P、Q、S构成的三角形，由此可得

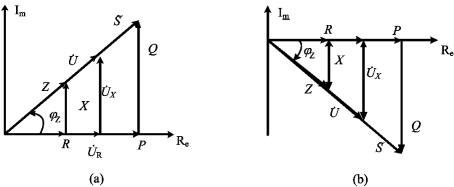
图5-30　功率三角形、电压三角形、阻抗三角形

对于无源或有源一端口电路，利用式（5-56）可以将其所吸收的复功率用电路的等效阻抗和等效导纳表示为

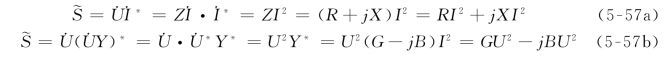
显然，由上式直接可以得出

其中，无功功率Q的符号与等效电抗X的符号相同，而与等效电纳B符号相反，这是由于等效电抗的符号与等效电纳的符号相反。

由式（5-56）还可以看出，无源或有源一端口电路吸收的有功功率P、无功功率Q以及视在功率S，在电流有效值不变的情况下，分别与等效电阻R、等效电抗X以及等效阻抗的模成正比，而在电压有效值不变的情况下，分别等效电导G或等效电纳B和等效导纳的模成正比。因而由等效电阻R、等效电抗X和等效阻抗的模为三边构成的阻抗三角形以及由等效电导G、等效电纳B和等效导纳的模为三边构成的导纳三角形，分别与功率三角形形成相似三角形。实际上，若将阻抗三角形的各边乘以电流I，就可得到电压三角形，将电压三角形的各边乘以电流I，就可得到功率三角形；而将导纳三角形的各边乘以电压U，就可得到电流三角形，将电流三角形的各边乘以电压U，就可得到功率三角形。因此，阻抗三角形、电压三角形及功率三角形是相似三角形；导纳三角形、电流三角形以及功率三角形也是相似三角形，如图5-30所示。

但要注意的是，复功率仅仅作为一个用于计算的复数量，并没有任何物理意义，即它不代表正弦量，也不直接反映时域范围内的内在能量关系。

例5-18　求图5-31所示电路中各支路吸收的复功率。

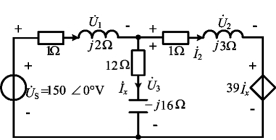
图5-31　例5-18图

解　根据KVL，有

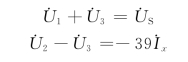
即

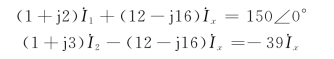
根据KCL，有

联立求解以上三式得

(www.daowen.com)

所以各支路电压为

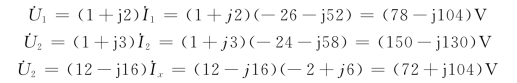
各支路吸收的复功率为

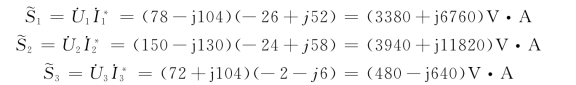
受控源支路吸收的复功率

独立电源发出的复功率

独立电源吸收的复功率

例5-19　电路如图5-32所示，求两负载吸收的总复功率，并求输入电流和总功率因数。

解　先求每一个负载的复功率

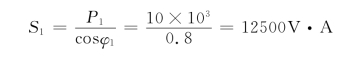
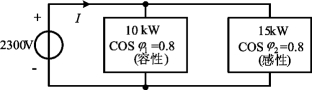
图5-32　例5-19图

Q1=S1sinφ1=S1sin（-arccos0.8）=12500sin（-36.9°）=-7500VAR

所以，有

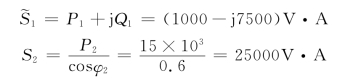
Q2=S2sinφ2=S2sin（-arccos0.6）=12500sin（53.1°）=20000VAR

得

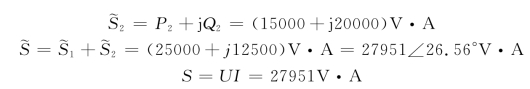
输入电流为

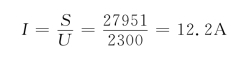
总的功率因数为

cosφ=cos26.56°=0.8945，呈感性