由于在正弦稳态电路分析中引入了阻抗的概念,因此,电阻电路中的欧姆定律、基尔霍夫定律的时域形式和其相量域形式完全一致,而电路分析的基本依据就是元件的伏安关系和基尔霍夫电压、电流定律,因此电阻电路的所有分析方法均可应用于正弦稳态电路,只是在电路相量模型中,电感元件和电容元件这两种元件的“电阻”分别用其阻抗ZL=jωL和![]()
![]() 表示,电阻仍然由R表示,独立电源和受控电源用其相量模型表示,电压和电流变量也用相量表示。这种将正弦稳态电路时域模型中的各电压、电流用相应的电压、电流相量表示,各电路元件都用其相量模型表示,可得到正弦稳态电路的相量模型(Phasor Domain Model)。基于正弦稳态电路相量模型建立的各种方程都是频域下的线性代数方程,称之为相量方程(Phasor Equation),可以采用类似电阻电路分析方法进行分析。这种基于相量模型对正弦稳态电路进行分析的方法称为相量分析法(Phasor Analysis),也称为正弦稳态电路的一般分析法或方程法。
表示,电阻仍然由R表示,独立电源和受控电源用其相量模型表示,电压和电流变量也用相量表示。这种将正弦稳态电路时域模型中的各电压、电流用相应的电压、电流相量表示,各电路元件都用其相量模型表示,可得到正弦稳态电路的相量模型(Phasor Domain Model)。基于正弦稳态电路相量模型建立的各种方程都是频域下的线性代数方程,称之为相量方程(Phasor Equation),可以采用类似电阻电路分析方法进行分析。这种基于相量模型对正弦稳态电路进行分析的方法称为相量分析法(Phasor Analysis),也称为正弦稳态电路的一般分析法或方程法。
列写相量域电路模型方程的主要步骤为:
(1)将时域电路变换为相量模型;
(2)根据相量形式的基尔霍夫定律(或节点分析法和回路分析法)和元件的伏安关系、等效变换以及电路定理等电阻电路的各种分析方法,建立电路的相量方程;
(3)用复数运算法则求解相量方程;
(4)将所得到的相量解,用相量反变换求出解的时域表达式。
例5-9 用节点分析法求如图5-19所示电路中的电流˙I。
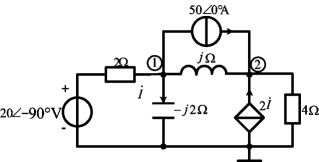
图5-19 例5-9图
解 设节点①和②的电压分别为˙U1和˙U2,对它们列写节点电压方程,有
对节点①:
![]()
对节点②:
![]()
补充方程为
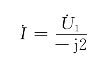
联立求解上述三个方程,得
![]()
例5-10 电路如图5-20(a)所示,已知![]() ,试求i1(t)和i2(t)。
,试求i1(t)和i2(t)。
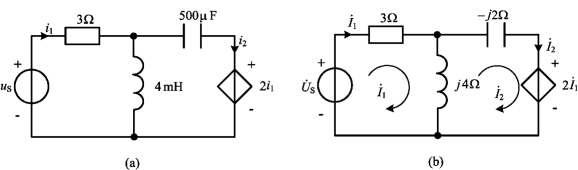
图5-20 例5-10图
解 图5-20(a)电路对应的相量模型如图5-20(b)所示,其中![]() ,
,![]()
![]() ,
,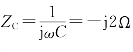 。根据网孔分析法,可得
。根据网孔分析法,可得
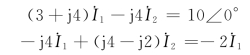
利用复数计算可得
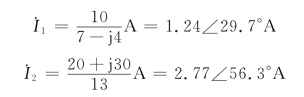
所求的电流为
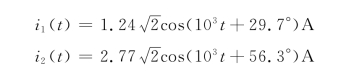
例5-11 图5-21所示电路中,已知Z=10+j50Ω,Z1=400+j1000Ω。问β等于多少时,![]() 和
和![]() 相位差为90°。
相位差为90°。
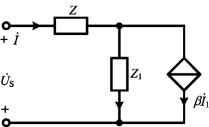
图5-21 例5-11图
解 由KVL,有
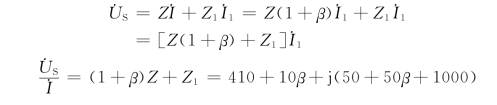 (https://www.daowen.com)
(https://www.daowen.com)
若上式的实部为零,则![]() 和
和![]() 相位差为90°。所以,令410+10β=0,则得β=-41,故有
相位差为90°。所以,令410+10β=0,则得β=-41,故有
![]() ,故电流领先电压90°。
,故电流领先电压90°。
例5-12 求图5-22(a)所示电路中的电流iL。已知图中电压源uS=10.![]()
![]() ,电流源
,电流源![]() 。
。
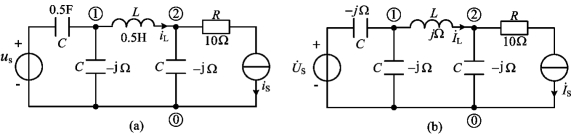
图5-22 例5-12图
解 电路中的电源为同一频率,则有
![]() ,可得图5-22(a)所示电路的相量模型电路如图5-22(b)所示。下面采用不同方法求解。
,可得图5-22(a)所示电路的相量模型电路如图5-22(b)所示。下面采用不同方法求解。
方法一:用节点分析法求解
取节点0作为参考节点,则节点①和②方程为
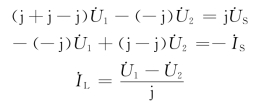
可解得
![]()
![]()
方法二:用网孔分析法求解
设自左到右3个网孔电流分别为![]() ,绕行方向为顺时针方向,则网孔电流方程为
,绕行方向为顺时针方向,则网孔电流方程为
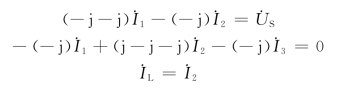
联立求得
![]()
方法三:用叠加定理求解
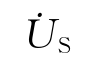 单 独 作 用 时
单 独 作 用 时
![]()
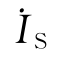 单独作用时
单独作用时
![]()
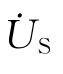 和
和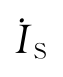 共 同 作 用 时
共 同 作 用 时
![]()
方法四:用戴维南定理求解
端口①—②的开路电压˙Uoc为
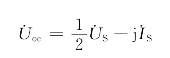
端口①—②的等效阻抗Zeq为
![]()
解得
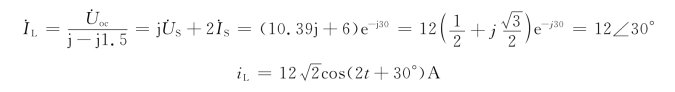
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







