1.正弦量的相量表示

图5-4所示为一RLC串联电路，根据KVL，有uR+uL+uC=uS其 中，uR=Ri，，，将这些式子代入上式，得

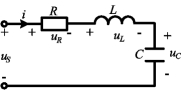
图5-4　RLC串联电路

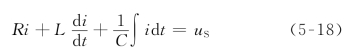
由数学理论可知，当激励uS为正弦量时，方程式（5-18）中的电流i的特解也一定是与uS同一频率的正弦量，反之亦然。这就是说，线性非时变电路在正弦电源激励下，各电路电压、电流的特解都是与激励同频率的正弦量，当电路中存在多个同频率的正弦激励时，该结论也成立。工程上将电路的这一特解称为正弦电流电路的稳定状态，简称正弦稳态（Sinusoidal Steady State）。电路处于正弦稳态时，同频率的各正弦量之间，仅在有效值、初相上存在“差异和联系”，这种“差异和联系”正是正弦稳态分析求解中的关键问题。下面以式（5-18）的求解为例，从理论上说明相量法的基础。

设式（5-18）中的激励源uS为

则电流i的特解将是与激励源uS同一频率的正弦量，因此，可设为

式中，I、φi——待求量。

将上述正弦量代入式（5-18）中，得

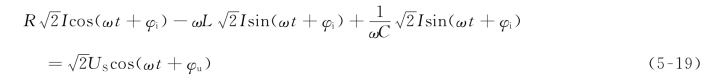
上述方程说明，正弦稳态电路方程是一组同频正弦函数描述的代数方程，电路基本定律所涉及的正弦电压、电流的运算，不会改变电压、电流同频正弦量的性质，即正弦量乘以常数、正弦量的微分、正弦的积分和正弦量的代数和等运算，其结果仍为同频率的正弦量，这就验证了前述的结论。

根据RLC电路在正弦激励下响应的求解过程可知，求微分方程的特解是比较麻烦的，对于复杂的电路，求解就更加麻烦。但若采用相量法，则求解就特别简单。相量法是建立在用复数来表示正弦量的基础上的，也就是建立在欧拉恒等式的基础上的。

设任一电路激励或响应变量作为正弦量f（t）的表达式为

根据欧拉公式，则有

所以，正弦量f（t）与复指数量Fmej（ωt+φ）之间的关系为

可见，式（5-22）中Fmejφ为一复常数，它是由正弦量的两个要素构成，即Fmejφ的模和幅角φ分别是正弦量f（t）的振幅和初相位。在正弦稳态分析中，将此复常数称为振幅相量，用表示正弦量f（t）的字母f对应的大写字母F加上表示最大值下标符号m，并加上一点即来表示，即

由于激励频率ω为已知，因此，只要确定了模和幅角φ，可以不用考虑ejωt，能够完全表征正弦稳态电路中的响应或激励正弦量。相量符号之所以上方加有一个圆点“·”，正是为了将其区别于一般的复常数，即相量对应于一个正弦量的复数。所以，对于正弦电压其对应的振幅相量为，有效值相量为；对于正弦电流，其对应的振幅相量为，有效值相量为。

由于表示正弦量的相量是一个复数，所以，它在几何上可以用复平面上的一条有向线段来表示，其长度表示复数的模，代表正弦量的幅值或有效值，幅角代表正弦量的初相位。这种在复平面上表示相量的矢量图称为相量图。

例5-1　已 知i1=-5cos（314t+60°）A，i2=10sin（314t+60°）A，i3=4cos（314t+60°）A。

（1）写出上述各电流的相量，并绘出它们的相量图；（2）求i1与i2和i1与i3的相位差；（3）绘出i1的波形；（4）若将i1表达式中的负号去掉将意味着什么？（5）求i1周期T和频率f。

解　本书根据国家标准，统一用cosine函数表示正弦量，为此要将不符合标准形式的正弦量表达式化为标准形式。

（1）i1=-5cos（314t+60°）=5cos（314t+60°-180°）=5cos（314t-120°）A

i2=10sin（314t+60°）=10cos（314t+60°-90°）=10cos（314t-30°）A

故i1、i2和i3的相量表示为

其相量图如图5-5（a）所示。

（2）求相位差

φ12=φ1-φ2=-120°-（-30°）=-90°

φ13=φ1-φ3=-120°-60°=-180°

（3）i1（t）的波形图如图5-5（b）所示。

（4）若将i1表达式中的负号去掉，意味着将i1反向。

（5）i1（t）的周期和频率分别为

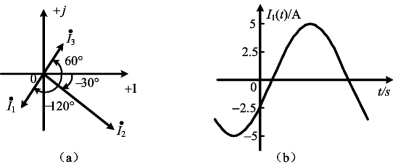
图5-5　例5-1图

2.相量变换的性质

根据相量的定义，可以推导出相量的几个常用运算性质。这几个运算性质对于应用相量法分析正弦稳态电路是非常重要的。

性质1　唯一特性

当且仅当两个同频率的正弦量用相同的相量表示，它们才是相等的。亦即对所有时刻t，有

证明：（1）充分性。由于表明在所有时刻t

根据复数相等的定义可知

（2）必要性

由于对所有时刻t，有

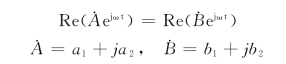
则在t=0时，由于，可得

即

a1=b1(www.daowen.com)

又，在时，由于，可得

所以

a2=b2

故根据复数相等的定义，可知

唯一性的含义是指正弦量与其相量是一一对应的，也就是说，根据正弦量可唯一地确定一个相量；同样，根据相量，当频率已知时，可以唯一地确定正弦量。

性质2　线性特性

设正弦量为

即

又设α1和α2为两个实数，则正弦量α1f1（t）+α2f2（t）可用相量表示。

证明：

由于对任何复数z1和z2，有

αiRezi=Re（αizi） i=1，2

和

α1Rez1+α2Rez2=Re（α1z1+α2z2）

可知

因此

亦即正弦量α1f1（t）+α2f2（t）可用相量表示。

线性特性说明相量变换和相量反变换都是线性变换，它有两个含义，即

（1）齐次性。它表明如果正弦量增大α倍，则其相量也增大α倍。

（2）相加性。它表明几个同频率正弦量之和的相量等于各个正弦量的相量之和。

例5-2　已知i1（t）=4cos（ωt+30°）A，i2（t）=5sin（ωt-20°）A，求它们的和。

解　电流i1（t）=4cos（ωt+30°）A为标准形式，其相量为

电流i2（t）为非标准形式，要把它转换为标准形式，即

i2（t）=5sin（ωt-20°）A=5cos（ωt-20°-90°）A=5cos（ωt-110°）A

则其相应的相量为

令i（t）=i1（t）+i2（t），则

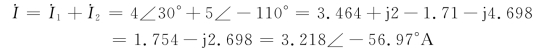
将其置换到时域，可得

i（t）=3.218cos（ωt-56.97°）A

性质3　微分特性

若任一正弦量f（t）=Fmcos（ωt+φ）所对应的振幅相量为，则正弦量所对应的幅值相量为。亦即。

证明：

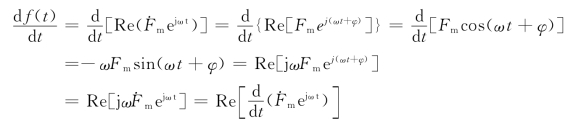
微分特性包含了两个内容：取实部和求导数运算是可以交换的；正弦量的n阶导数的相量等于该正弦量的相量乘以（jω）n。

性质4　积分特性

若任一正弦量f（t）=Fmcos（ωt+φ）所对应的振幅相量为，则正弦量积分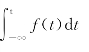所对应的幅值相量为。亦即。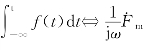

证明：

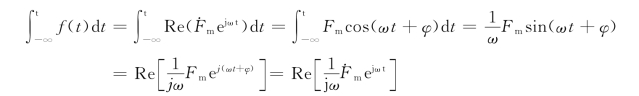
积分特性包含了两个内容：取实部和求积分运算是可以交换的；正弦量的n重积分相量等于该正弦量的相量除以（jω）n。

由相量的微分特性和积分特性可知，相量变换可以把微分和积分运算变换成复数的代数运算，而这正是相量法的优点所在。

例5-3　已知电路的微分方程为

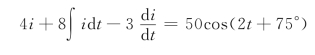
试求i（t）。

解　将方程中每一项从时域转换到频域，得

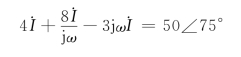
因为ω=2，所以

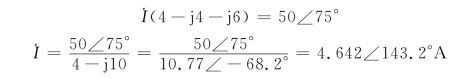
将上述相量转换到时域，得

i（t）=4.642cos（2t+143.2°）A